(本小题满分12分)已知等差数列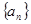 的第二项为8,前10项和为185.
的第二项为8,前10项和为185.
(1)求数列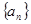 的通项公式;
的通项公式;
(2)若从数列 通项满足
通项满足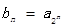 ,试求数列
,试求数列 的通项公式和前n项的和
的通项公式和前n项的和 .:
.:
已知函数
(1)求函数f(x)的极值
(2)求函数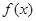 在
在 上的最大值和最小值.
上的最大值和最小值.
设复数z=(m2+2m-3)+(m-1)i, 试求m取何值时
(1)Z是实数;
(2)Z是纯虚数;
(3)Z对应的点位于复平面的第一象限.
(本小题满分13分)在平面直角坐标系中,已知三个点的坐标分别为: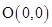 ,
,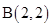 ,
,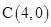 .
.
(1)若过点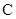 作一条直线
作一条直线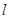 ,使点
,使点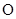 和点
和点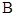 到直线
到直线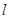 的距离相等,求直线
的距离相等,求直线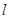 的方程;
的方程;
(2)求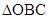 的外接圆的方程.
的外接圆的方程.
(本小题满分15分)如图,正方形 的边长为1,正方形
的边长为1,正方形 所在平面与平面
所在平面与平面 互相垂直,
互相垂直, 是
是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: ;
;
(3)求三棱锥 的体积.
的体积.
(1)利用“五点法”画出函数 在长度为一个周期的闭区间的简图
在长度为一个周期的闭区间的简图
(2)并说明该函数图象可由y=sinx(x R)的图象经过怎样平移和伸缩变换得到的。
R)的图象经过怎样平移和伸缩变换得到的。