下列关于星星的图案构成一个数列
，
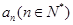对应图中星星的个数.
（1）写出
的值及数列的通项公式；
（2）求出数列
的前n项和
；
（3）若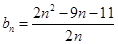
，对于（2）中的，有
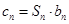，求数列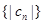
的前n项和
；
已知函数
，
（1）求函数f (x)的最小值和最小正周期；
（2）设△ABC的内角A、B、C的对应边分别为
、b、c，且
，若向量
共线，求、b的值；
已知
，
，
，
.
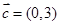（1）若
，求
；
（2）求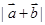
的取值范围；
（本题满分12分，每小题6分）
（1）若
为基底向量，且
若A、B、D三点共线，求实数k的值；
（2）用“五点作图法”在已给坐标系中画出函数
一个周期内的简图，并指出该函数图象是由函数
的图象进行怎样的变换而得到的？
（本小题满分14分）设函数
。
（1）若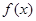
在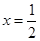
处取得极值，求
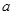的值；
（2）若在定义域内为增函数，求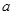的取值范围；
（3）设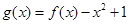
，当
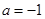时，
求证：①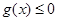 
在其定义域内恒成立；
求证：②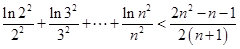 
。
为等比数列，
是等差数列，
的通项公式及前
项和
；
，
，其中
，试比较
与
的大小，并加以证明.