(本题满分12分,每小题6分)
(1)若 为基底向量,且
为基底向量,且 若A、B、D三点共线,求实数k的值;
若A、B、D三点共线,求实数k的值;
(2)用“五点作图法”在已给坐标系中画出函数 一个周期内的简图,并指出该函数图象是由函数
一个周期内的简图,并指出该函数图象是由函数 的图象进行怎样的变换而得到的?
的图象进行怎样的变换而得到的?
(本小题满分12分)
已知数列 满足
满足 ,点
,点 在直线
在直线 上.
上.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列 满足
满足
求
 的值;
的值;
(Ⅲ)对于(II)中的数列 ,求
,求 的值
的值
(本小题满分12分)
已知梯形 中,
中, ∥
∥ ,
, ,
, ,
, 、
、 分别是
分别是 上的点,
上的点, ∥
∥ ,
, ,
, 是
是 的中点。沿
的中点。沿 将梯形
将梯形 翻折,使平面
翻折,使平面 ⊥平面
⊥平面 (如图) .
(如图) .
(Ⅰ)当 时,求证:
时,求证: ;
;
(Ⅱ)以 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为 ,求
,求 的最大值;
的最大值;
(Ⅲ)当 取得最大值时,求钝二面角
取得最大值时,求钝二面角 的余弦值.
的余弦值.
(本小题满分12分)
小张参加了清华大学、上海交大、浙江大学三个学校的自主招生考试,各学校是否通过相互独立,其通过的概率分别为 、
、 、
、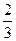 (允许小张同时通过多个学校)
(允许小张同时通过多个学校)
(1)小张没有通过任何一所学校的概率;
(2)设小张通过的学校个数为ξ,求ξ的分布列和它的数学期望。
(本小题满分12分)
设函数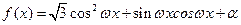 (其中
(其中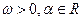 ),且
),且 的图象在
的图象在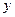 轴右侧的第一个最高点的横坐标为
轴右侧的第一个最高点的横坐标为 。
。
(Ⅰ)求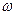 的值。
的值。
(Ⅱ)如果 在区间
在区间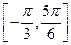 上的最小值为
上的最小值为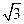 ,求
,求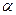 的值。
的值。
((本小题12分)
已知椭圆的一个顶点为(-2,0),焦点在x轴上,且离心率为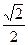 .
.
(1)求椭圆的标准方程.
(2)斜率为1的直线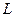 与椭圆交于A、B两点,O为原点,
与椭圆交于A、B两点,O为原点,
当△AOB的面积最大时,求直线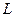 的方程.
的方程.