((本小题12分)
已知椭圆的一个顶点为(-2,0),焦点在x轴上,且离心率为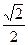 .
.
(1)求椭圆的标准方程.
(2)斜率为1的直线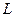 与椭圆交于A、B两点,O为原点,
与椭圆交于A、B两点,O为原点,
当△AOB的面积最大时,求直线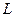 的方程.
的方程.
(本小题满分14分) 已知函数 及正整数数列
及正整数数列 . 若
. 若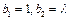 ,且当
,且当 时,有
时,有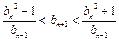 ; 又
; 又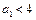 ,
, ,且
,且 对任意
对任意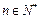 恒成立. 数列
恒成立. 数列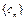 满足:
满足: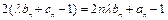 .
.
(1) 求数列 及
及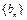 的通项公式;
的通项公式;
(2) 求数列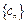 的前
的前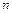 项和
项和 ;
;
(3) 证明存在 ,使得
,使得 对任意
对任意 均成立.
均成立.
(本小题满分12分) 设不等式组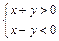 表示的平面区域为
表示的平面区域为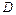 ,区域
,区域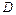 内的动点
内的动点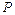 到直线
到直线 和直线
和直线 的距离之积为2, 记点
的距离之积为2, 记点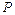 的轨迹为曲线
的轨迹为曲线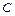 . 是否存在过点
. 是否存在过点 的直线l, 使之与曲线
的直线l, 使之与曲线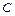 交于相异两点
交于相异两点 、
、 ,且以线段
,且以线段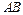 为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.
为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.
(本小题满分12分)如图,在四棱锥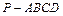 中,
中,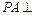 底面
底面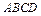 ,
,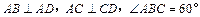 ,
,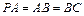 ,
, 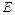 是
是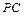 的中点.
的中点.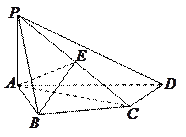 (1)证明
(1)证明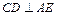 ;
;
(2)证明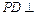 平面
平面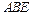 ;
;
(3)求二面角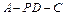 的大小.
的大小.
(本小题满分12分) 已知函数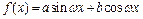 (
(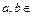 R,且
R,且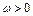 )的部分图象如图所示.
)的部分图象如图所示.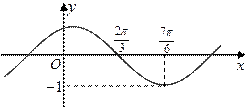
(1) 求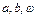 的值;
的值;
(2) 若方程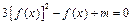
在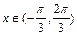 内有两个不同的解,求实数m的取值范围.
内有两个不同的解,求实数m的取值范围.
(本题满分12分)在九江市教研室组织的一次优秀青年教师联谊活动中,有一个有奖竞猜的环节.主持人准备了A、B两个相互独立的问题,并且宣布:幸运观众答对问题A可获奖金1000元,答对问题B可获奖金2000元,先答哪个题由观众自由选择,但只有第一个问题答对,才能再答第二题,否则终止答题.若你被选为幸运观众,且假设你答对问题A、B的概率分别为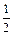 、
、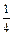 .
.
(1) 记先回答问题A的奖金为随机变量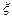 , 则
, 则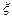 的取值分别是多少?
的取值分别是多少?
(2) 你觉得应先回答哪个问题才能使你获得更多的奖金?请说明理由.