(本小题满分12分) 设不等式组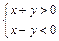 表示的平面区域为
表示的平面区域为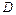 ,区域
,区域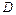 内的动点
内的动点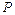 到直线
到直线 和直线
和直线 的距离之积为2, 记点
的距离之积为2, 记点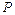 的轨迹为曲线
的轨迹为曲线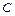 . 是否存在过点
. 是否存在过点 的直线l, 使之与曲线
的直线l, 使之与曲线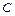 交于相异两点
交于相异两点 、
、 ,且以线段
,且以线段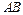 为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.
为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.
若函数y=f(x)的定义域是[0,2],求函数g(x)=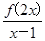 的定义域.
的定义域.
求函数y=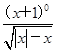 的定义域;
的定义域;
求下列函数的定义域:
(1) y= +lg(3x+1);
+lg(3x+1);
(2) y= .
.
已知二次函数f(x)=ax2+bx(a、b为常数,且a≠0)满足条件:f(x-1)=f(3-x),且方程f(x)=2x有等根.
(1)求f(x)的解析式;
(2)是否存在实数m、n(m<n),使f(x)定义域和值域分别为[m,n]和[4m,4n]?如果存在,求出m、n的值;如果不存在,说明理由.
已知函数f(x)=x2-4,设曲线y=f(x)在点(xn,f(xn))
处的切线与x轴的交点为(xn+1,0)(n∈N+),其中x1为正实数.
(1)用xn表示xn+1;
(2)求证:对一切正整数n,xn+1≤xn的充要条件是x1≥2;
(3)若x1=4,记an=lg  ,证明数列{an}成等比数列,并求数列{xn}的通项公式.
,证明数列{an}成等比数列,并求数列{xn}的通项公式.