已知二次函数f(x)=ax2+bx(a、b为常数,且a≠0)满足条件:f(x-1)=f(3-x),且方程f(x)=2x有等根.
(1)求f(x)的解析式;
(2)是否存在实数m、n(m<n),使f(x)定义域和值域分别为[m,n]和[4m,4n]?如果存在,求出m、n的值;如果不存在,说明理由.
已知等比数列 为正项递增数列,且
为正项递增数列,且 ,
,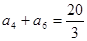 ,数列
,数列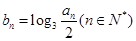 .
.
(1)求数列 的通项公式;
的通项公式;
(2) ,求
,求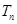 .
.
已知曲线 的参数方程是
的参数方程是 (
( 为参数),以坐标原点
为参数),以坐标原点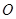 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线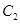 的极坐标方程是
的极坐标方程是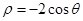 .
.
(1)写出 的极坐标方程和
的极坐标方程和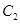 的直角坐标方程;
的直角坐标方程;
(2)已知点 、
、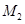 的极坐标分别是
的极坐标分别是 、
、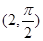 ,直线
,直线 与曲线
与曲线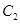 相交于
相交于 、
、 两点,射线
两点,射线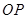 与曲线
与曲线 相交于点
相交于点 ,射线
,射线 与曲线
与曲线 相交于点
相交于点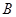 ,求
,求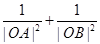 的值.
的值.
如图: 是⊙
是⊙ 的直径,
的直径, 是弧
是弧 的中点,
的中点, ⊥
⊥ ,垂足为
,垂足为 ,
, 交
交 于点
于点 .
.
(1)求证: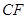 =
= ;
;
(2)若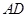 =4,⊙
=4,⊙ 的半径为6,求
的半径为6,求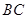 的长.
的长.
已知椭圆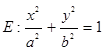 (a>b>0)的离心率为
(a>b>0)的离心率为 ,且过点(
,且过点(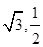 ).
).
(1)求椭圆E的方程;
(2)设直线l:y=kx+t与圆 (1<R<2)相切于点A,且l与椭圆E只有一个公共点B.
(1<R<2)相切于点A,且l与椭圆E只有一个公共点B.
①求证: ;
;
②当R为何值时,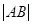 取得最大值?并求出最大值.
取得最大值?并求出最大值.
平行四边形 中,
中, ,
, ,且
,且 ,以BD为折线,把△ABD折起,
,以BD为折线,把△ABD折起, ,连接AC.
,连接AC.
(1)求证:;
(2)求二面角B-AC-D的大小.