如图: 是⊙
是⊙ 的直径,
的直径, 是弧
是弧 的中点,
的中点, ⊥
⊥ ,垂足为
,垂足为 ,
, 交
交 于点
于点 .
.
(1)求证: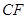 =
= ;
;
(2)若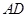 =4,⊙
=4,⊙ 的半径为6,求
的半径为6,求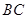 的长.
的长.
如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.
(1)求证:平面EBD⊥平面SAC;
(2)设SA=4,AB=2,求点A到平面SBD的距离;
如图,正三棱柱ABC—A1B1C1的底面边长的3,侧棱AA1=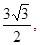 D是CB延长线上一点,且BD=BC.
D是CB延长线上一点,且BD=BC.
(Ⅰ)求证:直线BC1//平面AB1D;
(Ⅱ)求二面角B1—AD—B的大小;
(Ⅲ)求三棱锥C1—ABB1的体积.
下列五个正方体图形中,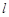 是正方体的一条对角线,点M,N,P分别为其所在棱的中点,求能得出
是正方体的一条对角线,点M,N,P分别为其所在棱的中点,求能得出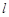 ⊥面MNP的图形的序号(写出所有符合要求的图形序号)
⊥面MNP的图形的序号(写出所有符合要求的图形序号)

如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′—EC—B是直二面角.
(1)证明:BE⊥C D′;
(2)求二面角D′—BC—E的正切值.
如图,已知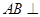 平面
平面 ,
,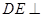 平面
平面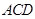 ,△
,△ 为等边三角形,
为等边三角形, ,
,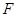 为
为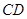 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面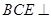 平面
平面 ;
;
(3)求直线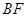 和平面
和平面 所成角的正弦值.
所成角的正弦值.