(本小题满分12分)
小张参加了清华大学、上海交大、浙江大学三个学校的自主招生考试,各学校是否通过相互独立,其通过的概率分别为 、
、 、
、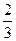 (允许小张同时通过多个学校)
(允许小张同时通过多个学校)
(1)小张没有通过任何一所学校的概率;
(2)设小张通过的学校个数为ξ,求ξ的分布列和它的数学期望。
已知函数 , ,其中 是自然对数的底数.
(Ⅰ)求曲线 在点 处的切线方程;
(Ⅱ)令 ,讨论 的单调性并判断有无极值,有极值时求出极值.
已知 是各项均为正数的等比数列,且 , .
(Ⅰ)求数列 的通项公式;
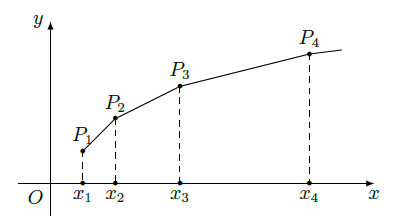
(Ⅱ)如图,在平面直角坐标系 中,依次连接点 , 得到折线 , 求由该折线与直线 , , 所围成的区域的面积 .
在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A 1 , A 2 , A 3 , A 4 , A 5 , A 6和4名女志愿者B 1 , B 2 , B 3 , B 4 , 从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(Ⅰ)求接受甲种心理暗示的志愿者中包含A 1但不包含B 1的概率.
(Ⅱ)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
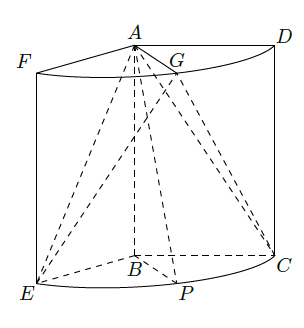
如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是 的中点.
(Ⅰ)设P是 上的一点,且 ,求 的大小;
(Ⅱ)当 , 时,求二面角 的大小.
设函数 ,其中 ,已知 .
(Ⅰ)求 ;
(Ⅱ)将函数 的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移 个单位,得到函数 的图象,求 在 上的最小值.