(本小题满分14分)一个几何体是由圆柱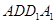 和三棱锥
和三棱锥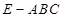 组合而成,点
组合而成,点 、
、 、
、 在圆
在圆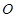 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图2所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图2所示,其中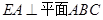 ,
,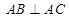 ,
, ,
, .
.
(1)求证: ;
;
(2)求三棱锥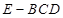 的体积.
的体积.
(本小题满分12分)在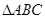 中,角
中,角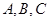 的对边分别为
的对边分别为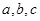 ,且
,且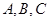 成等差数列。
成等差数列。
(Ⅰ)若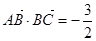 ,且
,且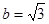 ,求
,求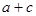 的值;
的值;
(Ⅱ)求 的取值范围。
的取值范围。
设函数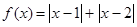 .
.
(1)画出函数y=f(x)的图像;
(2)若不等式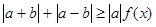 ,(a¹0,a、bÎR)恒成立,求实数x的范围.
,(a¹0,a、bÎR)恒成立,求实数x的范围.
(本小题满分10分)在直角坐标平面内,以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线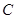 的极坐标方程是
的极坐标方程是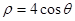 ,直线
,直线 的参数方程是
的参数方程是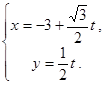 (
(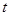 为参数)。
为参数)。
求极点在直线 上的射影点
上的射影点 的极坐标;
的极坐标;
若 、
、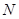 分别为曲线
分别为曲线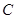 、直线
、直线 上的动点,求
上的动点,求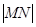 的最小值。
的最小值。
(本小题满分10分)从⊙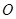 外一点
外一点 引圆的两条切线
引圆的两条切线 ,
, 及一条割线
及一条割线 ,
, 、
、 为切点.求证:
为切点.求证:
已知函数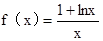
若函数在区间(a,a+ )上存在极值,其中a>0,求实数a的取值范围;
)上存在极值,其中a>0,求实数a的取值范围;
如果当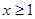 时,不等式
时,不等式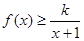 恒成立,求实数
恒成立,求实数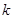 的取值范围。
的取值范围。