(本小题满分12分)
如图,在四棱锥S - ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA ="AB=BC" =2,AD =1.M是棱SB的中点.
(Ⅰ)求证:AM∥面SCD;
(Ⅱ)求面SCD与面SAB所成二面角的余弦值;
(Ⅲ)设点N是直线CD上的动点,MN与面SAB所成的角为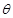 ,求sin
,求sin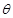 的最大值,
的最大值,
在△ABC中,内角A,B,C所对的边分别为a,b,c,cos B=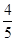 .
.
(1)求cos(A+C)的值;
(2)求sin 的值;
的值;
(3)若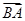 ·
·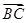 =20,求△ABC的面积.
=20,求△ABC的面积.
在△ABC中,内角A,B,C所对的边分别为a,b,c,且f(A)=2cos 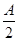 sin
sin +sin2
+sin2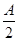 -cos2
-cos2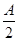 .
.
(1)求函数f(A)的最大值;
(2)若f(A)=0,C= ,a=
,a=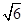 ,求b的值.
,求b的值.
已知函数f(x)=2 sin xcos x+2cos2x+m在区间
sin xcos x+2cos2x+m在区间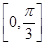 上的最大值为2.
上的最大值为2.
(1)求常数m的值;
(2)在△ABC中,内角A,B,C所对的边分别为a,b,c,若f(A)=1,sin B=3sin C,△ABC的面积为 ,求边长a.
,求边长a.
等比数列{cn}满足cn+1+cn=10·4n-1(n∈N*),数列{an}的前n项和为Sn,且an=log2cn.
(1)求an,Sn;
(2)数列{bn}满足bn=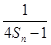 ,Tn为数列{bn}的前n项和,是否存在正整数m(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.
,Tn为数列{bn}的前n项和,是否存在正整数m(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.
数列{an}中,a1=3,an+1=an+cn(c是常数,n=1,2,3,…),且a1,a2,a3成公比不为1的等比数列.
(1)求c的值;
(2)求数列{an}的通项公式.