(本小题满分14分)
如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA,AC、CB、BP的中点.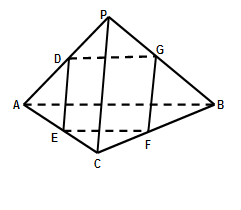
(1)求证:D、E、F、G四点共面;
(2)求证:PC⊥AB;
(3)若△ABC和△PAB都是等腰直角三角形,且AB=2,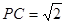 ,求四面体PABC的体积.
,求四面体PABC的体积.
.【必做题】本题满分10分.解答时应写出文字说明、证明过程或演算步骤.
由数字1,2,3,4组成五位数 ,从中任取一个.
,从中任取一个.
(1)求取出的数满足条件:“对任意的正整数 ,至少存在另一个正整数
,至少存在另一个正整数 ,且
,且 ,使得
,使得 ”的概率;
”的概率;
(2)记 为组成该数的相同数字的个数的最大值,求
为组成该数的相同数字的个数的最大值,求 的概率分布列和数学期望.
的概率分布列和数学期望.
.选修4—4:极坐标与参数方程
将参数方程 为参数
为参数 化为普通方程.
化为普通方程.
选修4—1:矩阵与变换
已知二阶矩阵A有特征值 及对应的一个特征向量
及对应的一个特征向量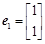 和特征值
和特征值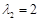 及对应
及对应
的一个特征向量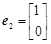 ,试求矩阵A.
,试求矩阵A.
.(本小题满分16分)
数列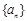 中,
中, ,
,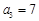 ,且
,且 .
.
(1)求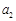 及
及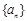 的通项公式;
的通项公式;
(2)设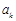 是
是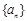 中的任意一项,是否存在
中的任意一项,是否存在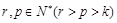 ,使
,使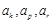 成等比数列?如存在,试分别写出
成等比数列?如存在,试分别写出 和
和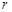 关于
关于 的一个表达式,并给出证明;
的一个表达式,并给出证明;
(3)证明:对一切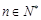 ,
,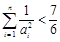 .
.
.(本小题满分16分)
函数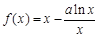 ,其中
,其中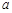 为常数.
为常数.
(1)证明:对任意 ,函数
,函数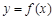 图像恒过定点;
图像恒过定点;
(2)当 时,不等式
时,不等式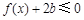 在
在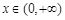 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)若对任意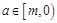 时,函数
时,函数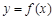 在定义域上恒单调递增,求
在定义域上恒单调递增,求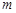 的最小值.
的最小值.