甲.乙两人在某公司做见习推销员,推销“小天鹅”洗衣机,他们在1~8月份的销售情况如下表所示:
| 月份 |
1月 |
2月 |
3月 |
4月 |
5月 |
6月 |
7月 |
8月 |
| 甲的销售量(单位:台) |
7 |
8 |
6 |
7 |
6 |
6 |
7 |
7 |
| 乙的销售量(单位:台) |
5 |
6 |
5 |
6 |
7 |
7 |
8 |
9 |
(1)在给出的坐标系中,绘制甲.乙两人这8个月的月销售量的折线图:(甲用实线;乙用虚线)
(2)请根据(1)中的折线图,写出2条关于甲.乙两人在这8个月中的销售状况的信息. ① ;② .
如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D. 点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s)。
(1)当x为何值时,PQ⊥AC,x为何值时,PQ⊥AB;
(2)设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式;
(3)当0<x<2时,求证:AD平分△PQD的面积。
在直角坐标系XOY中,二次函数图像的顶点坐标为 ,且与x轴的两个交点间的距离为6.
,且与x轴的两个交点间的距离为6.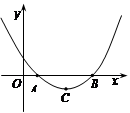
(1)求二次函数解析式;
(2)在x轴上方的抛物线上,是否存在点Q,使得以点Q、A、B为顶点的三角形与△ABC相似?如果存在,请求出Q点的坐标,如果不存在,请说明理由。
已知:关于x的一元二次方程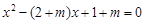
(1)求证:方程有两个实数根;
(2)设m<0,且方程的两个实数根分别为
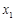 ,
,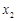 (其中
(其中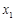 <
<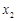 ),若y是关于m的函数,且
),若y是关于m的函数,且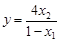 ,求这个函数的解析式;
,求这个函数的解析式;(3)在(2)的条件下,利用函数图象求关于m的方程
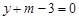 的解。
的解。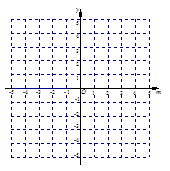
如图,在△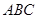 中,
中,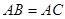 ,以
,以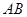 为直径的⊙O分别交
为直径的⊙O分别交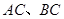 于点
于点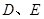 , 点
, 点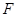 在
在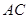 的延长线上,且
的延长线上,且 ∠
∠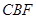
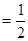 ∠
∠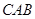 。
。
(1) 求证:AB⊥BF
(2) 若
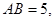 sin∠CBF=
sin∠CBF=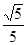 ,求BC和BF的长。
,求BC和BF的长。
某商场经销一种高档水果,如果每千克盈利10元,每天可出售500千克,经调查发现在进价不变的情况下,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,同时又要顾客得到实惠,那么每千克应涨价多少元?