(本小题满分14分)
我市有甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.
(1)设在甲家租一张球台开展活动 小时的收费为
小时的收费为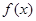 元
元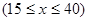 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动 小时的收费为
小时的收费为 元
元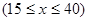 ,试求
,试求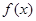 和
和 。
。
(2)问:小张选择哪家比较合算?说明理由。
14分)
(1)已知 是奇函数,求常数m的值;
是奇函数,求常数m的值;
(2)画出函数 的图象,并利用图象回答:
的图象,并利用图象回答:
k为何值时,方程|3x-1|=k无解?有一解?有两解?
(本小题满分12分)
为应对金融危机,刺激消费,某市给市民发放旅游消费卷,由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表:
  |
200元 |
300元 |
400元 |
500元 |
| 老年 |
0.4 |
0.3 |
0.2 |
0.1 |
| 中年 |
0.3 |
0.4 |
0.2 |
0.1 |
| 青年 |
0.3 |
0.3 |
0.2 |
0.2 |
某天恰好有持有这种消费卷的老年人、中年人、青年人各一人到该旅游景点,
(Ⅰ)求这三人消费总额大于1300元的概率;
(Ⅱ)设这三人中消费额大于300元的人数为 ,求
,求 的分布列及数学期望。
的分布列及数学期望。
(本小题满分12分)
如图, 在直三棱柱ABC-A1B1C1中,AC=3 ,BC=4,
,BC=4, ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求二面角 的余弦值.
的余弦值.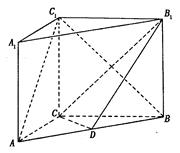
(本小题满分14分)
设函数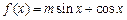
 的图象经过点
的图象经过点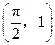 .
.
(Ⅰ)求 的解析式,并求函数的最小正周期和最值.
的解析式,并求函数的最小正周期和最值.
(Ⅱ)若 ,其中
,其中 是面积为
是面积为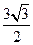 的锐角
的锐角 的内角,且
的内角,且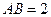 ,
,
求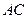 和
和 的长.
的长.
已知函数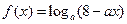
(1)若 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若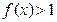 在区间[1,2]上恒成立,求实数
在区间[1,2]上恒成立,求实数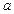 的取值范围.
的取值范围.