直线
与两坐标轴围成的三角形的面积为3，分别求满足下列条件的直线的方程.
（1）过定点
.
（2）与直线
垂直.
如图，AC为圆O的直径，弦BD⊥AC于点P，PC＝2，PA＝8，求tan∠ACD的值．
如图，点P在圆O直径AB的延长线上，且PB＝OB＝2，PC切圆O于C点，CD⊥AB于D点，求PC和CD的长．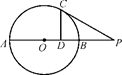
在梯形ABCD中，点E、F分别在腰AB、CD上，EF∥AD，AE∶EB＝m∶n.求证：(m＋n)EF＝mBC＋nAD.你能由此推导出梯形的中位线公式吗？
如图，四边形ABCD是正方形，E是AD上一点，且AE＝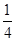
AD，N是AB的中点，NF⊥CE于F，求证：FN2＝EF·FC.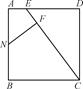
如图，在平行四边形ABCD中，E是CD的延长线上一点，BE与AD交于点F，DE＝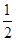
CD.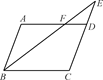
(1)求证：△ABF∽△CEB；
(2)若△DEF的面积为2，求平行四边形ABCD的面积．