在梯形ABCD中,点E、F分别在腰AB、CD上,EF∥AD,AE∶EB=m∶n.求证:(m+n)EF=mBC+nAD.你能由此推导出梯形的中位线公式吗?
已知数列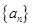 满足
满足 且
且 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)是否存在一个实数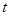 ,使得
,使得 且
且 为等差数列?若存在,求出
为等差数列?若存在,求出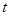 的值;
的值;
如不存在,请说明理由;
(Ⅲ)求数列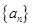 的前
的前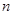 项和
项和 .
.
已知函数 .
.
(Ⅰ)求函数的最小正周期、最大值及取最大值时自变量的取值集合;
(Ⅱ)在 中,角
中,角 ,
, ,
, 的对边分别是
的对边分别是 ,
, ,
, ;若
;若 ,
, ,
, 成等比数列,且
成等比数列,且 ,
,
求 的值.
的值.
已知函数 (
(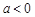 ).
).
(Ⅰ)若函数 在定义域内单调递增,求实数
在定义域内单调递增,求实数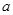 的取值范围;
的取值范围;
(Ⅱ)若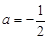 ,且关于
,且关于 的方程
的方程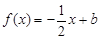 在
在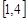 上恰有两个不等的实根,求实数
上恰有两个不等的实根,求实数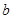 的取值范围;
的取值范围;
(Ⅲ)设各项为正数的数列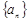 满足
满足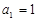 ,
,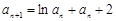 (
(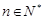 ),求证:
),求证: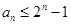 .
.
已知数列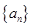 是各项均为正数的等差数列,其中
是各项均为正数的等差数列,其中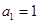 ,且
,且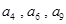 成等比数列;数列
成等比数列;数列 的前
的前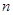 项和为
项和为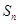 ,满足
,满足 .
.
(Ⅰ)求数列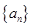 ,
, 的通项公式;
的通项公式;
(Ⅱ)如果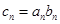 ,设数列
,设数列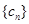 的前
的前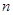 项和为
项和为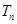 ,是否存在正整数
,是否存在正整数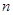 ,使得
,使得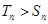 成立,若存在,
成立,若存在,
求出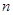 的最小值,若不存在,说明理由.
的最小值,若不存在,说明理由.
已知椭圆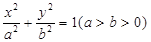 上的点
上的点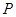 到左右两焦点
到左右两焦点 的距离之和为
的距离之和为 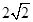 ,离心率为
,离心率为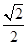 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过右焦点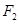 的直线
的直线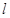 交椭圆于
交椭圆于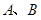 两点.
两点.
(ⅰ)若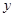 轴上一点
轴上一点 满足
满足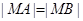 ,求直线
,求直线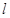 斜率
斜率 的值;
的值;
(ⅱ)是否存在这样的直线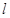 ,使
,使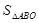 的最大值为
的最大值为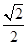 (其中
(其中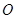 为坐标原点)?若存在,求直线
为坐标原点)?若存在,求直线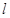 方
方
程;若不存在,说明理由.