如图,四边形ABCD是正方形,E是AD上一点,且AE=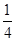 AD,N是AB的中点,NF⊥CE于F,求证:FN2=EF·FC.
AD,N是AB的中点,NF⊥CE于F,求证:FN2=EF·FC.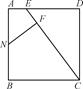
某中学调查了某班全部 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
(1)从该班随机选 名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的 名同学中,有5名男同学
名同学中,有5名男同学
 名女同学
名女同学 现从这
现从这 名男同学和
名男同学和 名女同学中各随机选
名女同学中各随机选 人,求
人,求 被选中且
被选中且 未被选中的概率.
未被选中的概率.
已知△ 的内角
的内角 所对的边分别为
所对的边分别为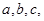 且
且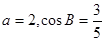 .
.
(1)若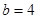 ,求
,求 的值;
的值;
(2)若△ 的面积
的面积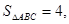 求
求 的值.
的值.
在平面直角坐标系 中,点
中,点 到两点
到两点 的距离之和等于4,设点
的距离之和等于4,设点 的轨迹为
的轨迹为 .
.
(1)写出曲线 的方程;
的方程;
(2)设直线 与曲线
与曲线 交于A、B两点,
交于A、B两点, 为何值时,
为何值时, ,此时
,此时 的值为多少?
的值为多少?
已知抛物线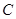 :
: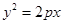
 过点
过点 .
.
(1)求抛物线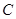 的方程,并求其准线方程;
的方程,并求其准线方程;
(2)是否存在平行于 (
(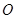 为坐标原点)的直线
为坐标原点)的直线 ,使得直线
,使得直线 与抛物线
与抛物线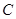 有公共点,且点
有公共点,且点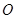 到
到 的距离等于
的距离等于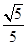 ?若存在求出直线
?若存在求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知函数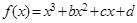 的图象过点
的图象过点 ,且在点
,且在点 处的切线方程为
处的切线方程为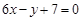 .
.
(1)求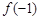 和
和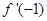 的值;
的值;
(2)求函数 的解析式.
的解析式.