某中学调查了某班全部 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
(1)从该班随机选 名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的 名同学中,有5名男同学
名同学中,有5名男同学
 名女同学
名女同学 现从这
现从这 名男同学和
名男同学和 名女同学中各随机选
名女同学中各随机选 人,求
人,求 被选中且
被选中且 未被选中的概率.
未被选中的概率.
已知函数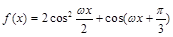 (其中
(其中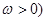 的最小正周期为
的最小正周期为 .
.
(Ⅰ)求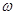 的值,并求函数
的值,并求函数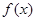 的单调递减区间;
的单调递减区间;
(Ⅱ)在锐角 中,
中,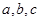 分别是角
分别是角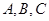 的对边,若
的对边,若
 的面积为
的面积为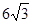 ,求
,求 的外接圆面积.
的外接圆面积.
已知数列 为等差数列,且
为等差数列,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足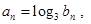 求数列
求数列 的前
的前 项和
项和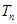 .
.
设函数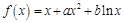 ,曲线
,曲线 过点
过点 ,且在
,且在 点处的切线斜率为2.
点处的切线斜率为2.
(1)求a和b的值; (2)证明: .
.
在△ABC中,角A,B,C的对边分别为a,b,c,已知 ,且C=120°.
,且C=120°.
(1)求角A;(2)若a=2,求c.
已知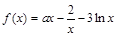 ,其中
,其中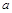 为常数.
为常数.
(Ⅰ)当函数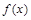 的图象在点
的图象在点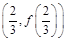 处的切线的斜率为1时,求函数
处的切线的斜率为1时,求函数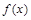 在
在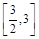 上的最小值;
上的最小值;
(Ⅱ)若函数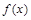 在
在 上既有极大值又有极小值,求实数
上既有极大值又有极小值,求实数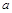 的取值范围;
的取值范围;
(Ⅲ)在(Ⅰ)的条件下,过点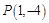 作函数
作函数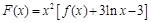 图象的切线,试问这样的切线有几条?并求这些切线的方程.
图象的切线,试问这样的切线有几条?并求这些切线的方程.