函数y=2cos(ωx+θ)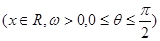
的图象与y轴交于点(0,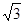 ),且该函数的最小正周期为π.
),且该函数的最小正周期为π.
(1)求θ和ω的值;
(2)已知点A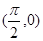 ,点P是该函数图象上一点,点Q(x0,y0)是PA的中点,当y0=
,点P是该函数图象上一点,点Q(x0,y0)是PA的中点,当y0=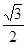 ,x0∈
,x0∈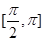 时,求x0的值.
时,求x0的值.
(本小题满分12分)
在一次人才招聘会上,有 三种不同的技工面向社会招聘,已知某技术人员应聘
三种不同的技工面向社会招聘,已知某技术人员应聘 三种技工被录用的概率分别是0.8、0.5、0.2(允许技工人员同时被多种技工录用).
三种技工被录用的概率分别是0.8、0.5、0.2(允许技工人员同时被多种技工录用).
(1)求该技术人员被录用的概率;
(2)设 表示该技术人员被录用的工种数与未被录用的工种数的乘积,求
表示该技术人员被录用的工种数与未被录用的工种数的乘积,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分10分)
在△ABC中,角A、B、C对边分别是 ,且满足
,且满足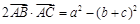 .
.
(1)求角A的大小;
(2)求 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小.
选修4-5:不等式选讲
已知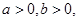 且
且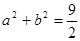 ,若
,若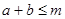 恒成立,
恒成立,
(Ⅰ)求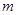 的最小值;
的最小值;
(Ⅱ)若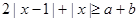 对任意的
对任意的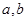 恒成立,求实数
恒成立,求实数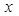 的取值范围.
的取值范围.
选修4-4:坐标系与参数方程
(Ⅰ)求直线 (
( 为参数)的倾斜角的大小.
为参数)的倾斜角的大小.
(Ⅱ)在极坐标系中,已知点 ,
, 是曲线
是曲线 上任意一点,求
上任意一点,求 的面积的最小值.
的面积的最小值.
选修4-2:矩阵与变换已知矩阵 ,向量
,向量 ,
,
(Ⅰ)求矩阵A的特征值和对应的特征向量;
(Ⅱ)求向量 ,使得
,使得 .
.