(本小题满分12分)已知双曲线 的两个焦点为
的两个焦点为 、
、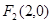 点
点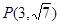 在双曲线C上.
在双曲线C上.
(1)求双曲线C的方程;
(2)记O为坐标原点,过点Q (0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为 求直线l的方程.
求直线l的方程.
(本小题满分8分)(1)不查表计算 +
+ ;
;
(2)解方程: 。
。
(本小题满分8分)某商品在近30天内每件的销售价格 (元)与时间
(元)与时间 天的函数关系是
天的函数关系是 该商品的日销售量
该商品的日销售量 (件)与时间
(件)与时间 (天)的函数关系是
(天)的函数关系是 (1),求这种商品的日销售额
(1),求这种商品的日销售额 的解析式,(2)求
的解析式,(2)求 的最大值.并指出日销售额的最大时是30天中的第几天
的最大值.并指出日销售额的最大时是30天中的第几天
21. (本小题满分12分)
已知函数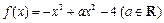 .
.
(1)若函数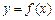 的图象在点P(1,
的图象在点P(1, )处的切线的倾斜角为
)处的切线的倾斜角为 ,求实数a的值;
,求实数a的值;
(2)设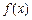 的导函数是
的导函数是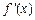 ,在 (1) 的条件下,若
,在 (1) 的条件下,若 ,求
,求 的最小值.
的最小值.
(3)若存在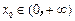 ,使
,使 ,求a的取值范围.
,求a的取值范围.
20. (本小题满分12分)
已知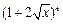 的展开式中,某一项的系数是它前一项系数的2倍,而等于它后一项的系数的
的展开式中,某一项的系数是它前一项系数的2倍,而等于它后一项的系数的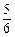 .
.
(1)求该展开式中二项式系数最大的项;
(2)求展开式中系数最大的项.
19. (本小题满分12分)
如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB = 60°的菱形,AC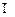 BD = O,A1C1
BD = O,A1C1 B1D1 = O1,E是O1A的中点.
B1D1 = O1,E是O1A的中点.
(1)求二面角O1-BC-D的大小;
(2)求点E到平面O1BC的距离.
|