(本小题满分14分)
已知椭圆的中心是坐标原点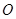 ,焦点在x轴上,离心率为
,焦点在x轴上,离心率为 ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为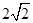 ,过点M(0,
,过点M(0, )与x轴不垂直的直线
)与x轴不垂直的直线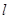 交椭圆于P、Q两点.
交椭圆于P、Q两点.
(1)求椭圆的方程;
(2)在y轴上是否存在定点N,使以PQ为直径的圆恒过这个点?若存在,求出N的坐标,若不存在,说明理由.
(本小题满分12分)
在△ABC中,已知 ,
, ,B=45°求
,B=45°求 及c 。
及c 。
(13分)
已知函数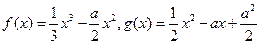 。
。
(I)当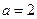 时,求曲线
时,求曲线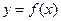 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当函数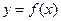 在区间
在区间 上的最小值为
上的最小值为 时,求实数
时,求实数 的值;
的值;
(Ⅲ)若函数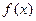 与
与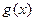 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数 的取值范围。
的取值范围。
. (12分)
已知函数f(x)= ,(p≠0)是奇函数.
,(p≠0)是奇函数.
(1)求m的值.
(2)若p>1,当x∈[1,2]时,求f(x)的最大值和最小值.
(12分)
已知a、b、c是互不相等的非零实数.
求证:三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0至少有一个方程有两个相异实根.
设复数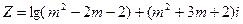 ,试求实数m取何值时
,试求实数m取何值时
(1)Z是实数;
(2)Z是纯虚数;
(3)Z对应的点位于复平面的第一象限