(本小题满分14分)
已知函数f (x)=ex,g(x)=lnx,h(x)=kx+b.
(1)当b=0时,若对 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
(2)设h(x)的图象为函数f (x)和g(x)图象的公共切线,切点分别为(x1, f (x1))和(x2, g(x2)),其中x1>0.
①求证:x1>1>x2;
②若当x≥x1时,关于x的不等式ax2-x+xe +1≤0恒成立,求实数a的取值范围.
+1≤0恒成立,求实数a的取值范围.
已知椭圆C: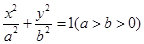 过点
过点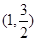 ,且椭圆C的离心率为
,且椭圆C的离心率为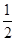 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若动点P在直线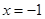 上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线
上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线 .证明:直线
.证明:直线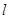 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.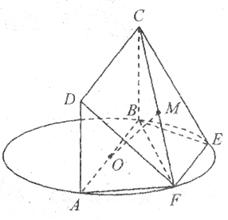
(Ⅰ)求证:AF⊥平面CBF;
(Ⅱ)设FC的中点为M,求证:OM∥平面DAF;
(Ⅲ)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为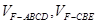 ,求
,求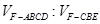 .
.
某高校在2012年的自主招生考试中随机抽取了100名学生的笔试成绩,按成绩分组:第一组[160,165),第二组[165,170),第三组[170,175),第四组[175,180),第五组[180,185)得到的频率分布直方图如图所示.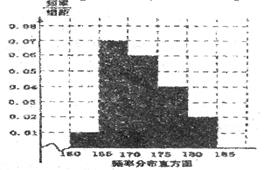
(1)求第三、四、五组的频率;
(2)为了以选拔出最优秀的学生,学校决定在笔试成绩高的第三、四、五组中用分层抽样抽取6名学生进入第二轮面试,求第三、四、五组每组各抽取多少名学生进入第二轮面试.
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第四组至少有一名学生被甲考官面试的概率.
已知函数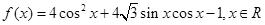 .
.
(1)求函数的最小正周期、最大值及取最大值时自变量的取值集合;
(2)在△ABC中,角A,B,C的对边分别是a,b,c;若a,b,c成等比数列,且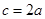 ,求
,求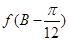 的值.
的值.
设函数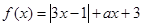 .
.
(1)若 时,解不等式
时,解不等式 ;
;
(2)若函数 有最小值,求a的取值范围.
有最小值,求a的取值范围.