数列 的前
的前 项和记为
项和记为 ,且满足
,且满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求和 ;
;
(3)设有 项的数列
项的数列 是连续的正整数数列,并且满足:
是连续的正整数数列,并且满足: .
.
问数列 最多有几项?并求这些项的和.
最多有几项?并求这些项的和.
设二次函数f(x)=x2+ax+a,方程f(x)-x=0的两根x1和x2满足0<x1<x2<1.
(1)求实数a的取值范围;
(2)试比较f(0)·f(1)-f(0)与的大小,并说明理由
若函数f(x)对定义域中任意x均满足f(x)+f(2a-x)=2b,则称函数y=f(x)的图象关于点(a,b)对称.
(1)已知函数f(x)=的图象关于点(0,1)对称,求实数m的值;
(2)已知函数g(x)在(-∞,0)∪(0,+∞)上的图象关于点(0,1)对称,且当x∈(0,+∞)时,g(x)=x2+ax+1,求函数g(x)在(-∞,0)上的解析式;
(3)在(1)(2)的条件下,当t>0时,若对任意实数x∈(-∞,0),恒有g(x)<f(t)成立,求实数a的取值范围.
函数f(x)=2x和g(x)=x3的图象的示意图如右图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.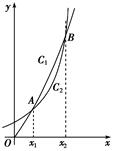
(1)请指出示意图中曲线C1,C2分别对应哪一个函数?
(2)若x1∈,x2∈,且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12}指出a,b的值,并说明理由;
(3)结合函数图象示意图,判断f(6),g(6),f(2010),g(2010)的大小.
设f(x)是定义在R上的奇函数,且对任意实数x恒满足f(x+2)=-f(x),当x∈[0,2]时,f(x)=2x-x2.
(1)求证:f(x)是周期函数.
(2)当x∈[2,4]时,求f(x)的解析式.
(3)计算f(0)+f(1)+f(2)+…+f(2011)
已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(1)求函数g(x)的解析式;
(2)解不等式g(x)≥f(x)-|x-1|;
(3)若h(x)=g(x)-λf(x)+1在[-1,1]上是增函数,求实数λ的取值范围