用配方法求证: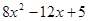 的值恒大于零.
的值恒大于零.
已知面包店的面包一个8元,小明去此店买面包,结账时店员告诉小明:“如果你再多买一个面包就可以打九折,价钱会比现在便宜16元”,小明说:“我买这些就好了,谢谢”,根据两人的对话,判断结账时小明买了多少个面包?
若多项式 的值与x的取值无关,求m的值.
的值与x的取值无关,求m的值.
解方程:
(1)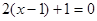
(2)
(3)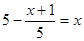
(4)
合并同类项:
(1)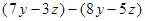
(2)
已知正方形ABCD的边长为4cm,有一动点P以1cm/s的速度沿A—B—C—D的路径运动,设P点运动的时间为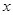 (s)(0<
(s)(0<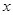 <12),△ADP的面积为
<12),△ADP的面积为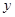 cm2.
cm2.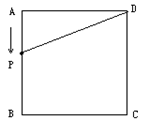
(1)求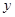 与
与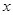 的函数关系式;
的函数关系式;
(2)在给定的平面直角坐标系中画出上述函数关系的图象; 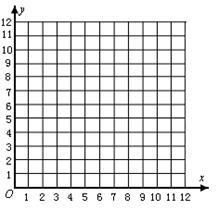
(3)点P运动多长时间时,△ADP是等腰三角形(只写结果).