某旅游团上午8时从旅馆出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离旅馆的距离S(千米)与时间t (时)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题: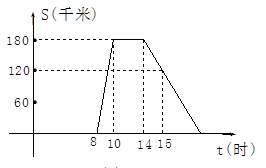
(1)求该团去景点时的平均速度是多少?
(2)该团在旅游景点游玩了多少小时?
(3)求出返程途中S(千米)与时间t (时)的函数关系式,并求出自变量t的取值范围.
两个全等的直角三角形重叠放在直线上,如图14-1,AB=6cm,BC=8cm,∠ABC=90°,将Rt△ABC在直线上向左平移,使点C从F点向E点移动,如图14-2所示.
(1)求证:四边形ABED是矩形;请说明怎样移动Rt△ABC,使得四边形ABED是正方形?
(2)求证:四边形ACFD是平行四边形;说明如何移动Rt△ABC,使得四边形ACFD为菱形?
(3)若Rt△ABC向左移动的速度是1cm/s,设移动时间为t秒,四边形ABFD的面积为Scm.求s随t变化的函数关系式.
种植草莓大户张华现有22吨草莓等售,现有两种销售渠道:一是运往省城直接批发给零售商;二是在本地市场零售.经过调查分析,这两种销售渠道每天销量及每吨所获纯利润见下表:
| 销售渠道 |
每日销量(吨) |
每吨所获纯利润(元) |
| 省城批发 |
4 |
1200 |
| 本地零售 |
1 |
2000 |
受客观因素影响,每天只能采用一种销售渠道,草莓必须在10日内售出.
(1)若一部分草莓运往省城批发给零售商,其余在本地市场零售,请写出销售22吨草莓所获纯利润y(元)与运往省城直接批发给零售商的草莓量x(吨)之间的函数关系式;
(2)由于草莓必须在10日内售完,请你求出x的取值范围;
(3)怎样安排这22吨草莓的销售渠道,才能使所获纯利润最大?并求出最大纯利润.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF、FD.
(1)求证:四边形AFDC是平行四边形;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了部分学生进行调查。对数据进行整理,得到下面两个都不完整的扇形统计图(图1)和条形统计图(图2):
(1)该校数学兴趣小组采取的调查方式是 (填“普查”或“抽样调查”);一共调查了名学生;
(2)求扇形统计图中的m,并补全条形统计图;
(3)求扇形统计图中,“乘私家车”所对应扇形的圆心角的度数;
(4)小明说:“为了调查方便,全部在同一个年级抽取.” 这样的抽样是否合理?请说明理由;
(5)根据调查的结果,估计全校2000名学生骑车上学有多少人?
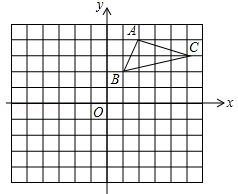
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标(,);
(2)将△ABC的三个顶点的横、纵坐标都乘以-1,分别得到对应点A2、B2、C2,画出△A2B2C2,则△ABC和△A2B2C2关于对称;
(3)将△ABC在网格中平移,使点B的对应点B3坐标为(-6,1),画出△A3B3C3.