动圆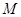 经过定点
经过定点 ,且与直线
,且与直线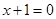 相切。
相切。
(1)求圆心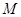 的轨迹
的轨迹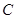 方程;
方程;
(2)直线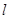 过定点
过定点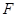 与曲线
与曲线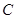 交于
交于 、
、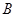 两点:
两点:
①若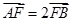 ,求直线
,求直线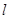 的方程;
的方程;
②若点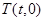 始终在以
始终在以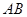 为直径的圆内,求
为直径的圆内,求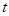 的取值范围。
的取值范围。
(本小题满分12分)如图,点A,B分别是椭圆 的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为:
的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为: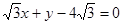 且
且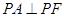 .
.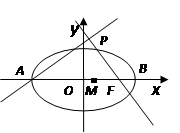
(1)求直线AP的方程;
(2)设点M是椭圆长轴AB上一点,点M到直线AP的距离等于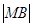 ,求椭圆上的点到点M的距离d的最小值.
,求椭圆上的点到点M的距离d的最小值.
(本小题满分12分)已知A,B两点是椭圆 与坐标轴正半轴的两个交点.
与坐标轴正半轴的两个交点.
(1)设 为参数,求椭圆的参数方程;
为参数,求椭圆的参数方程;
(2)在第一象限的椭圆弧上求一点P,使四边形OAPB的面积最大,并求此最大值.
(本小题满分12分)已知直线 的参数方程为
的参数方程为 (
( 为参数),若以直角坐标系
为参数),若以直角坐标系 的
的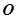 点为极点,
点为极点,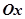 方向为极轴,选择相同的长度单位建立极坐标系,得曲线
方向为极轴,选择相同的长度单位建立极坐标系,得曲线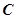 的极坐标方程为
的极坐标方程为
(1)将直线 的参数方程化为普通方程,把曲线
的参数方程化为普通方程,把曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若直线 与曲线
与曲线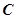 交于
交于 两点,求
两点,求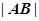 .
.
. (本小题满分12分)如图2所示,将一个长为8m,宽为5m的长方形剪去四个相同的边长为xm的正方形,然后再将所得图形围成一个无盖长方体,试求x为多少时,长方体的体积最大?最大体积为多少?
.(本小题满分10分)已知函数 .
.
(1)求这个函数的导数;
(2)求这个函数的图象在点 处的切线方程.
处的切线方程.