(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
(理)某种型号汽车四个轮胎半径相同,均为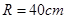 ,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为
,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为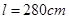 (假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路
(假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路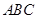 (如图(1)所示,其中
(如图(1)所示,其中 (
(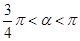 )),且前轮
)),且前轮 已在
已在 段上时,后轮中心在
段上时,后轮中心在 位置;若前轮中心到达
位置;若前轮中心到达 处时,后轮中心在
处时,后轮中心在 处(假定该汽车能顺利驶上该上坡路). 设前轮中心在
处(假定该汽车能顺利驶上该上坡路). 设前轮中心在 和
和 处时与地面的接触点分别为
处时与地面的接触点分别为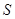 和
和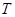 ,且
,且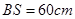 ,
,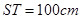 . (其它因素忽略不计)
. (其它因素忽略不计)
(1)如图(2)所示, 和
和 的延长线交于点
的延长线交于点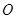 ,
,
求证: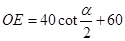 (cm);
(cm);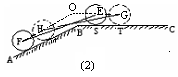
(2)当 =
=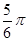 时,后轮中心从
时,后轮中心从 处移动到
处移动到 处实际移动了多少厘米? (精确到1cm)
处实际移动了多少厘米? (精确到1cm)
(本小题满分12分)已知四棱锥 中,底面ABCD为直角梯形,BC//AD,
中,底面ABCD为直角梯形,BC//AD, ,且PA=AB=BC=1,AD=2,
,且PA=AB=BC=1,AD=2, 平面ABCD,E为AB的中点.
平面ABCD,E为AB的中点.
(Ⅰ)证明: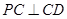 ;
;
(Ⅱ)在线段PA上是否存在一点F,使EF//平面PCD,若存在,求 的值.
的值.
(本小题满分12分)国家教育部要求高中阶段每学年都要组织学生进行“国家学生体质健康数据测试”,方案要求以学校为单位组织实施,某校对高一1班同学按照“国家学生体质健康数据测试”项目按百分制进行了测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请求出70~80分数段的人数;
(Ⅱ)现根据测试成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、 、第五组)中任意选出两人,形成搭档小组.若选出的两人成绩差大于20,则称这两人为“搭档组”,试求选出的两人为“搭档组”的概率.
(本小题满分12分)
已知函数 .
.
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)当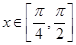 时,求函数
时,求函数 的最大值和最小值.
的最大值和最小值.
已知函数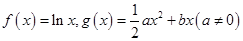 .
.
(Ⅰ)若 时,函数
时,函数 在其定义域上是增函数,求b的取值范围;
在其定义域上是增函数,求b的取值范围;
(Ⅱ)在(Ⅰ)的结论下,设函数 ,求函数
,求函数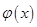 的最小值;
的最小值;
(Ⅲ)设函数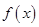 的图象
的图象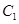 与函数
与函数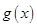 的图象
的图象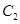 交于P、Q,过线段PQ的中点R作
交于P、Q,过线段PQ的中点R作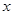 轴的垂线分别交
轴的垂线分别交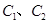 于点M、N,问是否存在点R,使
于点M、N,问是否存在点R,使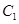 在M处的切线与
在M处的切线与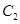 在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
在直角坐标系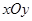 ,椭圆
,椭圆 的左、右焦点分别为
的左、右焦点分别为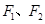 .其中
.其中 也是抛物线
也是抛物线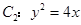 的焦点,点M为
的焦点,点M为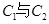 在第一象限的交点,且
在第一象限的交点,且 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若过点D(4,0)的直线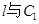 交于不同的两点A、B,且A在DB之间,试求
交于不同的两点A、B,且A在DB之间,试求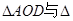 BOD面积之比的取值范围.
BOD面积之比的取值范围.