(本题满分14分,第1小题6分,第2小题8分)
已知函数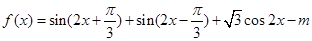 ,x∈R,且f(x)的最大值为1.
,x∈R,且f(x)的最大值为1.
(1) 求m的值,并求f(x)的单调递增区间;
(2) 在△ABC中,角A、B、C的对边a、b、c,若 ,且
,且 ,试判断△ABC的形状.
,试判断△ABC的形状.
(本小题10分)某宾馆有50个房间供游客居住,当每个房间定价为每天180元时,房间会全部住满;房间单价增加10元,就会有一个房间空闲,如果游客居住房间,宾馆每间每天需花费20元的各种维护费用。房间定价多少时,宾馆利润最大?
(本小题10分)设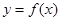 是二次函数,方程
是二次函数,方程 有两个相等的实根,且
有两个相等的实根,且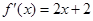 .
.
(1)求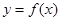 的表达式;
的表达式;
(2)若直线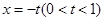 把
把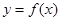 的图象与两坐标轴所围成图形的面积二等分,求
的图象与两坐标轴所围成图形的面积二等分,求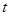 的值.
的值.
(本小题10分) 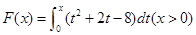 .
.
(1)求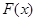 的单调区间;(2)求函数
的单调区间;(2)求函数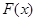 在
在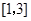 上的最值.
上的最值.
已知定圆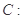
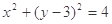 ,定直线
,定直线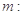
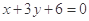 ,过
,过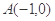 的一条动直线
的一条动直线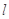 与直线相交于
与直线相交于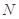 ,与圆
,与圆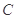 相交于
相交于 两点,
两点,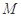 是
是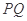 中点.
中点.
(Ⅰ)当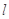 与
与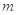 垂直时,求证:
垂直时,求证: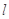 过圆心
过圆心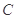 ;
;
(Ⅱ)当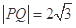 时,求直线
时,求直线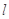 的方程;
的方程;
(Ⅲ)设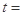
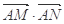 ,试问
,试问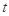 是否为定值,若为定值,请求出
是否为定值,若为定值,请求出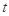 的值;若不为定值,请说明理由.
的值;若不为定值,请说明理由.
已知定义域为R的函数 是奇函数.
是奇函数.
①求m、n的值;
②若对任意的t∈ ,不等式
,不等式 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.