已知定圆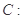
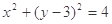 ,定直线
,定直线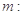
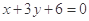 ,过
,过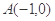 的一条动直线
的一条动直线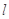 与直线相交于
与直线相交于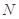 ,与圆
,与圆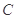 相交于
相交于 两点,
两点,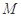 是
是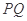 中点.
中点.
(Ⅰ)当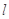 与
与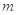 垂直时,求证:
垂直时,求证: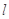 过圆心
过圆心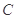 ;
;
(Ⅱ)当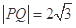 时,求直线
时,求直线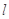 的方程;
的方程;
(Ⅲ)设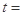
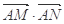 ,试问
,试问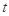 是否为定值,若为定值,请求出
是否为定值,若为定值,请求出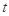 的值;若不为定值,请说明理由.
的值;若不为定值,请说明理由.
已知数列 的前
的前 项和为
项和为 ,向量
,向量 ,
, ,满足条件
,满足条件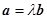 ,
, 且
且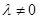 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设函数 ,数列
,数列 满足条件
满足条件 ,
,
①求数列 的通项公式;
的通项公式;
②设 ,求数列
,求数列 的前
的前 和
和 .
.
如图,一简单几何体的一个面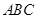 内接于圆
内接于圆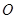 ,
,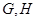 分别是
分别是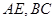 的中点,
的中点,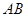 是圆
是圆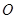 的直径,四边形
的直径,四边形 为平行四边形,且
为平行四边形,且 平面
平面 .
.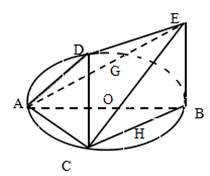
(1)求证: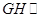 平面
平面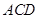 ;
;
(2)若AC=BC=BE=2,求二面角O-CE-B的余弦值.
在2014年11月4日宜宾市举办的四川省第十四届少数民族传统体育运动会的餐饮点上,某种茶饮料一天的销售量与该天的日平均气温(单位:℃)有关,若日平均气温不超过15 ℃,则日销售量为100瓶;若日平均气温超过15℃但不超过20 ℃,则日销售量为150 瓶;若日平均气温超过20 ℃,则日销售量为200瓶.据宜宾市气象部门预测,该地区在运动会期间每一天日平均气温不超过15 ℃,超过15 ℃但不超过20 ℃,超过20 ℃这三种情况发生的概率分别为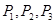 ,又知P1,P2为方程5x2-3x+a=0的两根,且
,又知P1,P2为方程5x2-3x+a=0的两根,且 .
.
(1)求P1,P2,P3的值;
(2)记ξ表示该茶饮料在运动会期间任意两天的销售量总和(单位:瓶),求 的分布列及数学期望.
的分布列及数学期望.
已知函数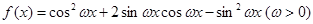 ,且周期为
,且周期为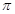 .
.
(1)求 的值;
的值;
(2)当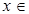 [
[ ]时,求
]时,求 的最大值及取得最大值时
的最大值及取得最大值时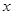 的值.
的值.
(本小题满分14分)设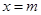 和
和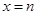 是函数
是函数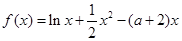 的两个极值点,其中
的两个极值点,其中 ,
, .
.
(1)若曲线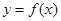 在点
在点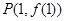 处的切线垂直于
处的切线垂直于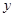 轴,求实数
轴,求实数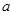 的值;
的值;
(2)求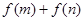 的取值范围;
的取值范围;
(3)若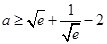 ,求
,求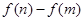 的最大值(
的最大值(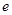 是自然对数的底数).
是自然对数的底数).