已知中心在原点，焦点在坐标轴上的椭圆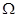
，它的离心率为
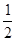，一个焦点和抛物线
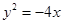的焦点重合,过直线
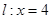上一点M引椭圆的两条切线，切点分别是A,B.
（Ⅰ）求椭圆的方程；
（Ⅱ）若在椭圆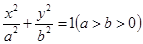
上的点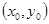
处的椭圆的切线方程是
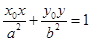. 求证:直线
恒过定点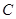
；并出求定点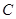的坐标.
（Ⅲ）是否存在实数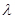
，使得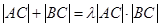
恒成立？(点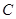为直线恒过的定点)若存在，求出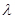的值；若不存在，请说明理由。
已知函数
满足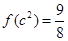
．
（1）求常数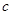
的值 ；
（2）解不等式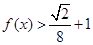
．
求曲线y=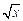
,
,
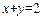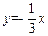围成的平面图形的面积.
已知p:方程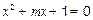
有两个不相等的负实根；q:不等式
的解集为R，若p∨q为真命题，p∧q为假命题，求m的取值范围。
（本题12分）某地区上年度电价为
元/kW•h，年用电量为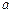
kW•h．本年度计划将电价降低到0．55元/ kW•h到0．75元/ kW•h之间，而用户期望电价为0．40元/ kW•h．经测算，下调电价后新增用电量与实际电价与用户的期望电价的差成反比（比例系数为
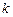），该地区电力的成本价为0．30元/ kW•h．
（1）写出本年度电价下调后，电力部门的收益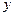
与实际电价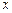
之间的函数关系式；
（2）设=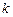
，当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%？（注：收益=实际电量×（实际电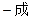价
本价））
（本题12分）已知全集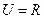
,集合A
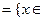R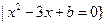
，
B={x∈R|(x-2)(x2+3x-4)=0}
（1）若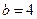
时，存在集合M使得A
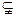M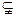B,求出所有这样的集合M；
（2）集合A、B是否能满足∁UB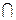
A=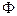
？若能，求实数
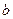的取值范围；若不能，请说明理由.