如图所示,直线OA与x轴成135°角,x轴上下方分别有水平向右的匀强电场E1和竖直向上的匀强电场E2,且电场强度E1=E2=10N/C,x轴下方还存在垂直于纸面向外的匀强磁场B,磁感应强度B=10T。现有一质量m=1.0×10-5kg,电荷量q=1.0×10-5C的带正电尘粒在OA直线上的A点静止释放,A点离原点O的距离d= m(g取10m/s2,).求:
m(g取10m/s2,).求:
(1)尘粒刚进入磁场区域时的速度v的大小;
(2)从进入磁场区域开始到离开磁场区域所经历的时间t;
(3)第一次回到OA直线上的某位置离原点O的距离L。
我国首个月球探测计划“嫦娥工程”将分三个阶段实施,大约用十年左右时间完成,这极大地提高了同学们对月球的关注程度,以下是某同学就有关月球的知识设计的两个问题,请你解答:
(1)若已知地球半径为R,地球表面的重力加速度为g,月球绕地球运动的周期为T,且把月球绕地球的运动近似看做是匀速圆周运动。试求出月球绕地球运动的轨道半径。
(2)若某位宇航员随登月飞船登陆月球后,在月球某水平表面上方h高处以速度 水平抛出一个小球,小球落回到月球表面的水平距离为s。已知月球半径为
水平抛出一个小球,小球落回到月球表面的水平距离为s。已知月球半径为 ,万有引力常量为
,万有引力常量为 。试求出月球的质量
。试求出月球的质量 。
。
如图甲所示,相隔一定距离的竖直边界两侧为相同的匀强磁场区,磁场方向垂直纸面向里,在边界上固定两长为L的平行金属极板MN和PQ,两极板中心各有一小孔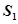 、
、 ,两极板间电压的变化规律如图乙所示,正反向电压的大小均为
,两极板间电压的变化规律如图乙所示,正反向电压的大小均为 ,周期为
,周期为 。在
。在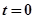 时刻将一个质量为
时刻将一个质量为 、电量为
、电量为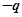 (
(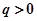 )的粒子由
)的粒子由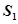 静止释放,粒子在电场力的作用下向右运动,在
静止释放,粒子在电场力的作用下向右运动,在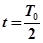 时刻通过
时刻通过 垂直于边界进入右侧磁场区。(不计粒子重力,不考虑极板外的电场)
垂直于边界进入右侧磁场区。(不计粒子重力,不考虑极板外的电场)
(1)求粒子到达 时的速度大小
时的速度大小 和极板距离
和极板距离
(2)为使粒子不与极板相撞,求磁感应强度的大小应满足的条件。
(3)若已保证了粒子未与极板相撞,为使粒子在t=2T0时刻再次到达 ,且速度恰好为零,求该过程中粒子在磁场内运动的周期。
,且速度恰好为零,求该过程中粒子在磁场内运动的周期。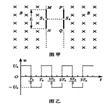
如图所示的滑轮,它可以绕垂直于纸面的光滑固定水平轴O转动,轮上绕有轻质柔软细线,线的一端系一质量为3m的重物,另一端系一质量为m,电阻为r的金属杆.在竖直平面内有间距为L的足够长的平行金属导轨PQ、EF,在QF之间连接有阻值为R的电阻,其余电阻不计,磁感应强度为Bo的匀强磁场与导轨平面垂直,开始时金属杆置于导轨下端QF处,将重物由静止释放,当重物下降h时恰好达到稳定速度而匀速下降.运动过程中金属杆始终与导轨垂直且接触良好,忽略所有摩擦,求: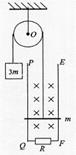
(1)重物匀速下降的速度v;
(2)重物从释放到下降h的过程中,电阻R中产生的焦耳热QR;
(3)若将重物下降h时的时刻记作t=0,速度计为v0,从此时刻起,磁感应强度逐渐减小,若此后金属杆中恰好不产生感应电流,则磁感应强度B怎样随时间t变化(写出B与t的关系式).
如图a所示,一个电阻值为R=1Ω,匝数为n=100的圆形金属线与阻值为2R的电阻R1连结成闭合回路。线圈的半径为r1=12cm. 在线圈中半径为r2=10cm的圆形区域存在垂直于线圈平面向里的匀强磁场,磁感应强度B随时间t变化的关系图线如图b所示。图线与横、纵轴的截距分别为t0=10s和B0=3T. 导线的电阻不计。求0至t1=6s的时间内
(a)
(1)通过电阻R1上的电流大小和方向;
(2)通过电阻R1上的电量q及电阻R1上产生的热量。
如图,一个质量为0.6kg 的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失)。已知圆弧的半径R=0.3m,θ="60" 0,小球到达A点时的速度 v="4" m/s。(取g ="10" m/s2)求:
(1)小球做平抛运动的初速度v0;
(2)P点与A点的水平距离和竖直高度;
(3)小球到达圆弧最高点C时对轨道的压力。