(12分)我们把同时满足下列两个性质的函数称为“和谐函数” :
①函数在整个定义域上是单调增函数或单调减函数;
②在函数的定义域内存在区间
,使得函数在区间
上的值域为
.
⑴已知幂函数
的图像经过点
,判断
是否是和谐函数?
⑵判断函数
是否是和谐函数?
⑶若函数
是和谐函数,求实数
的取值范围.
(本小题满分12分)
已知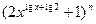
展开式中最后三项的系数的和是方程
的正数解，它的中间项是
，求
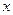的值．
(本小题满分10分)
设函数
（I）求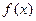
的最小值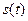
；
（II）若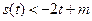
对
时恒成立，求实数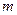
的取值范围.
(本小题满分12分）
在一个直径是50的球形器材中，嵌入一根圆轴（如图5-5），为了使圆轴不易脱出，
应该使它与球有最大的接触面积，问圆轴的半径x应是多少？
(本小题满分12分）
设函数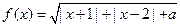
．
（Ⅰ）当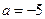
时，求函数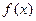
的定义域；
（Ⅱ）若函数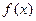的定义域为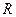
，试求实数
的取值范围．
(本小题满分10分）
在对人们的休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人.女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21
人主要的休闲方式是看电视，另外33人主要的休闲方式是运动.
（Ⅰ）根据以上数据建立一个2×2的列联表；
（Ⅱ）判断性别与休闲方式是否有关系.