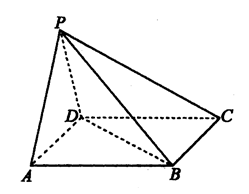
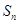如图,在四棱锥 中,底面
中,底面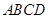 是正方形,侧面
是正方形,侧面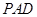 是正三角形,且平面
是正三角形,且平面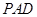 ⊥底面
⊥底面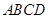
(1)求证: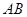 ⊥平面
⊥平面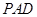
(2)求直线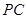 与底面
与底面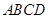 所成角的余弦值;
所成角的余弦值;
(3)设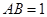 ,求点
,求点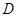 到平面
到平面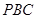 的距离.
的距离.
如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20 m,求山高CD.
数列{an}的首项为3,{bn}为等差数列且bn=an+1-an(n∈N*).若b3=-2,b10=12,求a8的值
已知函数y= cos2x+
cos2x+ sinxcosx+1,x∈R.
sinxcosx+1,x∈R.
(1)当函数y取得最大值时,求自变量x的集合;
(2)求该函数的的单调增区间
设各项均为正数的等比数列{an}中,a1+a3=10,a3+a5=40. 数列{bn}中,前n项和
(1)求数列{an}与{bn}的通项公式;
(2)若c1=1,cn+1=cn+ ,求数列
,求数列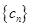 的通项公式
的通项公式
(3)是否存在正整数k,使得 +
+ +…+
+…+ >
>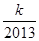 对任意正整数n均成立?若存在,求出k的最大值,若不存在,说明理由.
对任意正整数n均成立?若存在,求出k的最大值,若不存在,说明理由.
某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少.从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%.
(1)求第n年初M的价值an的表达式;
(2)求数列 的前n项和
的前n项和