已知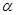 为第二象限的角,
为第二象限的角,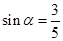 ,
,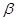 为第一象限的角,
为第一象限的角,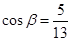 .求
.求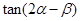
 的值.
的值.
(1)计算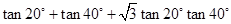 的值
的值
(2)化简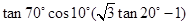
将背面相同正面分别标有1、2、3、4的四张卡片洗匀后背面朝上放在桌面上,(1)从中随机的抽取一张卡片,求该卡片正面上的数字是偶数的概率(2)先从中随机的抽取一张卡片(不放回),将该卡片正面上的数字作为十位数字,再随机的抽取一张卡片,将该卡片正面上的数字作为个位数字,则组成的两位数恰好是4的倍数的概率是多少?
设正有理数x是 的一个近似值,令
的一个近似值,令 。
。
(Ⅰ)若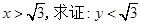 ;
;
(Ⅱ)比较y与x哪一个更接近于 ,请说明理由.
,请说明理由.
如图,A,B,C是圆O上三个点,AD是∠BAC的平分线,交圆O于点D,过B作圆O的切线交AD的延长线于E.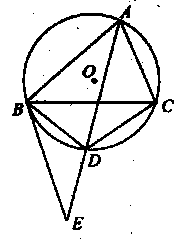
(Ⅰ)求证:∠EBD=∠CBD;
(II)求证:AB·DE=CD·BE.