.已知双曲线的中心在原点,对称轴为坐标轴,一条渐近线方程为 ,右焦点
,右焦点 ,双曲线的实轴为
,双曲线的实轴为 ,
,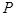 为双曲线上一点(不同于
为双曲线上一点(不同于 ),直线
),直线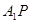 ,
, 分别与直线
分别与直线 交于
交于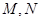 两点
两点
(1)求双曲线的方程;
(2)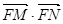 是否为定值,若为定值,求出该值;若不为定值,说明理由。
是否为定值,若为定值,求出该值;若不为定值,说明理由。
(本小题13分)已知定义在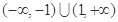 的奇函数满足:①
的奇函数满足:①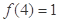 ;②对任意
;②对任意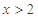 均有
均有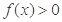 ;③对任意
;③对任意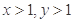 ,均有
,均有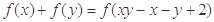 .
.
(Ⅰ)求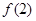 的值;
的值;
(Ⅱ)证明: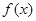 在
在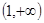 上为增函数;
上为增函数;
(Ⅲ)是否存在实数k,使得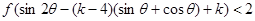 对任意的
对任意的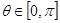 恒成立?若存在,求出的k范围;若不存在说明理由.
恒成立?若存在,求出的k范围;若不存在说明理由.
(本小题12分)已知函数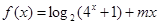 .
.
(Ⅰ)若 是偶函数,求实数m的值;
是偶函数,求实数m的值;
(Ⅱ)当 时,关于x的方程
时,关于x的方程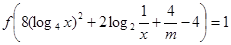 在区间
在区间 上恰有两个不同的实数解,求m的范围.
上恰有两个不同的实数解,求m的范围.
(本小题12分)已知函数 .
.
(Ⅰ)当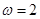 时,把
时,把 的图像向右平移
的图像向右平移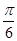 个单位得到函数
个单位得到函数 的图像,求函数
的图像,求函数 的图像的对称中心坐标;
的图像的对称中心坐标;
(Ⅱ)设 ,若
,若 的图象与直线
的图象与直线 的相邻两个交点之间的距离为π,求
的相邻两个交点之间的距离为π,求 的值,并求函数
的值,并求函数 的单调递增区间.
的单调递增区间.
(本小题13分)已知函数 在区间[-1,2]上的最大值是最小值的8倍.
在区间[-1,2]上的最大值是最小值的8倍.
(Ⅰ)求a的值;
(Ⅱ)当a>1时,解不等式 .
.
(本小题13分)平面内给定三个向量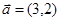 ,
,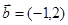 ,
,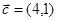 .
.
(Ⅰ)设向量 ,且
,且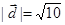 ,求向量
,求向量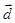 的坐标;
的坐标;
(Ⅱ)若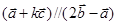 ,求实数k的值.
,求实数k的值.