(本小题13分)已知定义在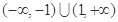 的奇函数满足:①
的奇函数满足:①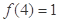 ;②对任意
;②对任意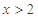 均有
均有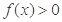 ;③对任意
;③对任意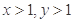 ,均有
,均有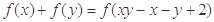 .
.
(Ⅰ)求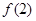 的值;
的值;
(Ⅱ)证明: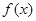 在
在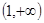 上为增函数;
上为增函数;
(Ⅲ)是否存在实数k,使得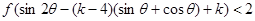 对任意的
对任意的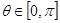 恒成立?若存在,求出的k范围;若不存在说明理由.
恒成立?若存在,求出的k范围;若不存在说明理由.
(本小题12分)设点 ,点A在y轴上移动,点B在x轴正半轴(包括原点)上移动,点M在AB连线上,且满足
,点A在y轴上移动,点B在x轴正半轴(包括原点)上移动,点M在AB连线上,且满足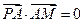 ,
, .
.
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)设轨迹C的焦点为F,准线为l,自M引的垂线,垂足为N,设点 使四边形PFMN是菱形,试求实数a;
使四边形PFMN是菱形,试求实数a; (Ⅲ)如果点A的坐标为
(Ⅲ)如果点A的坐标为 ,
,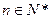 ,其中
,其中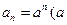 >
>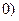 ,相应线段AM的垂直平分线交x轴于
,相应线段AM的垂直平分线交x轴于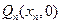 .设数列
.设数列 的前n项和为
的前n项和为 ,证明:当n≥2时,
,证明:当n≥2时, 为定值.
为定值.
(本小题满分12分)已知向量 =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量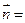 (2,0)所成角为
(2,0)所成角为 ,其中A, B, C是⊿ABC的内角.
,其中A, B, C是⊿ABC的内角.
(1)求角B的大小;(2)求sinA+sinC的取值范围.
(本小题满分12分)数列 的通项是关于
的通项是关于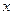 的不等式
的不等式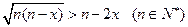 的解集中整数的个数,
的解集中整数的个数, (1)求数列
(1)求数列 的通项公式; (2)是否存在实数
的通项公式; (2)是否存在实数 使不等式
使不等式 对一切大于1的自然数
对一切大于1的自然数 恒成立,若存在试确定
恒成立,若存在试确定 的取值范围,否则说明原因.
的取值范围,否则说明原因.
(本小题满分14分)
设A(-2,0),B(2,0),M为平面上任一点,若|MA|+|MB|为定值,且cosAMB的最小值为-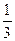 .
.
(1)求M点轨迹C的方程;(2)过点N(3,0)的直线l与轨迹C及单位圆x2+y2=1自右向左依次交于点P、Q、R、S,若|PQ|=|RS|,则这样的直线l共有几条?请证明你的结论.
(本小题满分12分)已知函数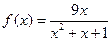 (
(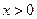 ) , (Ⅰ)试确定
) , (Ⅰ)试确定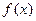 的单调区间 , 并证明你的结论 ;(Ⅱ)若
的单调区间 , 并证明你的结论 ;(Ⅱ)若 时 , 不等式
时 , 不等式 恒成立 , 求实数
恒成立 , 求实数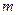 的取值范围 .
的取值范围 .