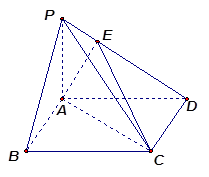
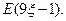如图,在四棱锥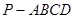 中,底面
中,底面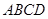 是边长为
是边长为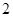 的正方形,
的正方形,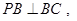
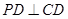 ,且
,且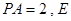 点满足
点满足 .
. 
(1)证明: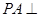 平面
平面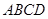 .
.
(2)在线段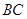 上是否存在点
上是否存在点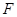 ,使得
,使得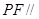 平面
平面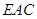 ?若存在,确定点
?若存在,确定点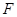 的位置,若不存在请说明理由 .
的位置,若不存在请说明理由 .
设函数
(1)若
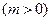 上的最大值
上的最大值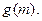
(2)若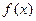 在区间[1,2]上为减函数,求a的取值范围。
在区间[1,2]上为减函数,求a的取值范围。
(3)若直线 为函数
为函数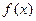 的图象的一条切线,求a的值。
的图象的一条切线,求a的值。
设直线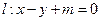 与抛物线
与抛物线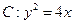 交于不同两点A、B,F为抛物线的焦点。
交于不同两点A、B,F为抛物线的焦点。
(1)求 的重心G的轨迹方程;
的重心G的轨迹方程;
(2)如果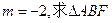 的外接圆的方程。
的外接圆的方程。
已知数列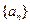 满足:
满足: 已知存在常数p,q使数列
已知存在常数p,q使数列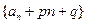 为等
为等
比数列。
(1)求常数p、q及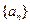 的通项公式;
的通项公式;
(2)解方程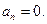
(3)求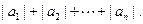
(本小题满分12分)
已知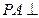 矩形ABCD所在平面,PA=AD=
矩形ABCD所在平面,PA=AD=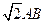 ,E为线段PD上一点。
,E为线段PD上一点。
(1)当E为PD的中点时,求证: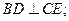
(2)是否存在E使二面角E—AC—D为30°?若存在,求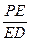 ,若不存在,说明理由。
,若不存在,说明理由。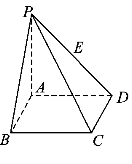
袋中有大小相 同的4个红球与2个白球。
同的4个红球与2个白球。
(1)若从袋中依次不放回取出一个球,求第三次取出白球的概率;
( 2)若从袋中依次不放回取出
2)若从袋中依次不放回取出 一个球,求第一次取出红球的条件下第三次仍取出红球的概率。
一个球,求第一次取出红球的条件下第三次仍取出红球的概率。
(3)若从中有放回的依次取出一个球,记6次取球中取出红球的次数为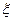 ,求
,求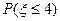 与
与