(本小题满分14分)
已知函数 ,
,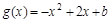
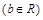 ,记
,记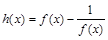 。
。
(Ⅰ)判断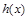 的奇偶性,并证明;
的奇偶性,并证明;
(Ⅱ)对任意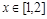 ,都存在
,都存在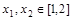 ,使得
,使得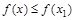 ,
,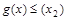 .若
.若 ,求实数
,求实数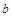 的值;
的值;
(Ⅲ)若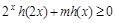 对于一切
对于一切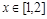 恒成立,求实数
恒成立,求实数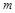 的取值范围.
的取值范围.
在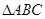 中,角
中,角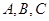 的对边分别为
的对边分别为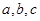 ,且
,且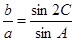 .
.
(1)若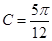 ,求角
,求角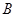 的大小;
的大小;
(2)若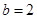 ,
,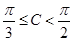 ,求
,求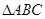 面积的最小值.
面积的最小值.
(本小题满分14分)已知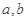 是实数,函数
是实数,函数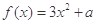 ,
,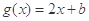 ,若
,若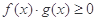 在区间
在区间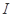 上恒成立,则称
上恒成立,则称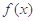 和
和 在区间
在区间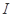 上为“
上为“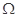 函数”.
函数”.
(1)设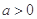 ,若
,若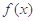 和
和 在区间
在区间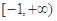 上为“
上为“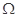 函数”,求实数
函数”,求实数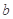 的取值范围;
的取值范围;
(2)设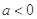 且
且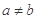 ,若
,若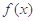 和
和 在以
在以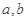 为端点的开区间上为“
为端点的开区间上为“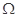 函数”,求
函数”,求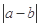 的最大值.
的最大值.
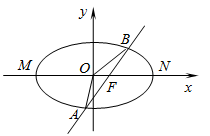
(本小题满分15分)若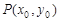
 是椭圆
是椭圆
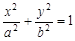
 上一点,
上一点, 分别是椭圆
分别是椭圆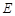 的左、右顶点,直线
的左、右顶点,直线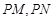 的斜率的乘积等于
的斜率的乘积等于 .
.
(1)求椭圆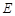 的离心率
的离心率 的值;
的值;
(2)过椭圆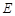 的右焦点F且斜率为1的直线交椭圆于
的右焦点F且斜率为1的直线交椭圆于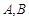 两点,
两点, 为坐标原点,若
为坐标原点,若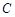 为椭圆上一点,满足
为椭圆上一点,满足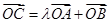 ,求实数
,求实数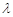 的值.
的值.
如图,平面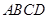 ⊥平面
⊥平面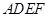 ,其中
,其中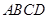 为矩形,
为矩形,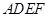 为梯形,
为梯形,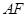 ∥
∥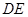 ,
,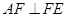 ,
, .
.
(1)求异面直线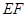 与
与 所成角的大小;
所成角的大小;
(2)若二面角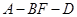 的平面角的余弦值为
的平面角的余弦值为 ,求
,求 的长.
的长.
(本小题满分14分)已知函数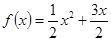 ,数列
,数列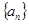 的前
的前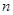 项的和为
项的和为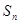 ,点
,点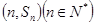 均在函数
均在函数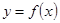 的图象上.
的图象上.
(1)求数列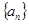 的通项公式
的通项公式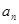 ;
;
(2)令 ,证明:
,证明: .
.