如图,平面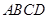 ⊥平面
⊥平面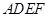 ,其中
,其中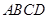 为矩形,
为矩形,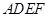 为梯形,
为梯形,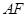 ∥
∥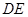 ,
,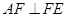 ,
, .
.
(1)求异面直线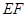 与
与 所成角的大小;
所成角的大小;
(2)若二面角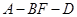 的平面角的余弦值为
的平面角的余弦值为 ,求
,求 的长.
的长.
设
是由
个实数组成的
行
列的数表,满足:每个数的绝对值不大于1,且所有数的和为零,记
为所有这样的数表构成的集合。
对于
,记
为
的第
行各数之和(
),
为
的第
列各数之和(
):
记
为
,
,…,
,
,
,…,
中的最小值。
对如下数表
,求
的值;
| 1 |
1 |
-0.8 |
| 0.1 |
-0.3 |
-1 |
(2)设数表
(2,3)形如
| 1 |
1 |
|
| -1 |
求
的最大值;
(3)给定正整数
,对于所有的
(2,2
+1),求
的最大值。
已知曲线
.
(1)若曲线
是焦点在x轴点上的椭圆,求
的取值范围;
(2)设
,曲线
与
轴的交点为
(点
位于点
的上方),直线
与曲线
交于不同的两点
,直线
与直线
交于点
.求证:
三点共线.
已知函数 , , .
(1)若曲线
与曲线
在它们的交点
处具有公共切线,求
的值
(2)当
时,若函数
的单调区间,并求其在区间
上的最大值.
近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱。为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| "厨余垃圾"箱 |
"可回收物"箱 |
"其他垃圾"箱 |
|
| 厨余垃圾 |
400 |
100 |
100 |
| 可回收物 |
30 |
240 |
30 |
| 其他垃圾 |
20 |
20 |
60 |
(Ⅰ)试估计厨余垃圾投放正确的概率
(Ⅱ)试估计生活垃圾投放错误的概率
(Ⅲ)假设厨余垃圾在"厨余垃圾"箱、"可回收物"箱、"其他垃圾"箱的投放量分别为
,其中
,
.当数据
的方差
最大时,写出
的值(结论不要求证明),并求此时
的值。
(注:
,其中
为数据
的平均数)
如图1,在
中,
,
,
,
分别
是上的点,且
,
,将
沿
折起到
的位置,使
,如图2.
(1)求证:
平面
;
(2)若
是
的中点,求
与平面
所成角的大小;
(3)线段
上是否存在点
,使平面
与平面
垂直?说明理由