(本小题满分13分)
已知抛物线、椭圆和双曲线都经过点 ,它们在
,它们在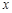 轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.
轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.
(1)求这三条曲线的方程;
(2)对于抛物线上任意一点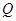 ,点
,点 都满足
都满足 ,求
,求 的取值范围.
的取值范围.
(本题满分 分)袋中有质地、大小完全相同的
分)袋中有质地、大小完全相同的 个球,编号分别为
个球,编号分别为 、
、 、
、 、
、 、
、 ,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢。
,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢。
(1) 求两个编号的和为6的概率;
(2)求甲赢的事件发生的概率.
(示范高中做)(本题满分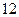 分)已知双曲线
分)已知双曲线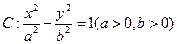 的离心率为
的离心率为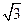 ,且双曲线上点到右焦点的距离与到直线
,且双曲线上点到右焦点的距离与到直线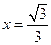 的距离之比为
的距离之比为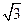
(1) 求双曲线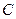 的方程;
的方程;
(2)已知直线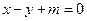 与双曲线
与双曲线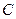 交于不同的两点
交于不同的两点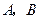 ,且线段
,且线段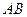 的中点在圆
的中点在圆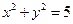 上,求
上,求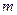 的值.
的值.
(普通高中做)(本题满分 分)已知抛物线的顶点在坐标原点,焦点在
分)已知抛物线的顶点在坐标原点,焦点在 轴正半轴,抛物线上一点
轴正半轴,抛物线上一点 到焦点的距离为
到焦点的距离为 ,求
,求 的值及抛物线方程.
的值及抛物线方程.
本题满分 分)已知命题
分)已知命题 :关于
:关于 的一元二次方程
的一元二次方程 有两个不相等的实数根,命题
有两个不相等的实数根,命题 :
:
 是增函数,若
是增函数,若 或
或 为真命题,
为真命题, 且
且 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
(本题满分 分)为了解高一学生的体
分)为了解高一学生的体
能情况,某校抽取部分学生进行一分钟跳
绳次数的测试,将所得数据整理、分组后,
画出频率分布直方图(如图).图中从左到右
各小长方形面积之比为 .
.
若第二组的频数为 .
.
(1) 求第二组的频率是多少?样本容量是
多少?
(2)若次数在 以上(含
以上(含 次)为达标,试估计该学校全体高一学生的达标率是多少?
次)为达标,试估计该学校全体高一学生的达标率是多少?