已知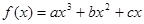 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间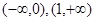 上是减函数,又
上是减函数,又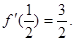
(Ⅰ)求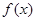 的解析式;
的解析式;
(Ⅱ)若在区间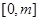 (m>0)上恒有
(m>0)上恒有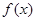 ≤
≤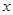 成立,求m的取值范围.
成立,求m的取值范围.
已知函数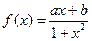 是定义在(-1,1)上的奇函数,且
是定义在(-1,1)上的奇函数,且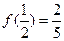 。
。
(1)试求出函数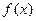 的解析式;
的解析式;
(2)证明函数在定义域内是单调增函数。
已知:命题p:x1和x2是方程x2-mx-2=0的两个实根,且不等式a2-5a-3≥|x1-x2|对任意实数m∈[-1,1]恒成立;命题q:函数y=lg(ax2-x+a)的定义域为R.
若命题p是假命题,命题q是真命题,求a的取值范围.
(1)判断函数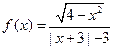 奇偶性,并给出证明;
奇偶性,并给出证明;
(2)求函数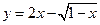 的值域。
的值域。
(本小题满分12分)
已知函数 R).
R).
(Ⅰ)若a=1,函数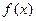 的图象能否总在直线
的图象能否总在直线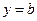 的下方?说明理由;
的下方?说明理由;
(Ⅱ)若函数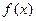 在(0,2)上是增函数,求a的取值范围;
在(0,2)上是增函数,求a的取值范围;
(Ⅲ)设 为方程
为方程 的三个根,且
的三个根,且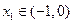 ,
, ,
, ,求证:
,求证: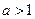 或
或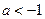
(本小题满分12分)
设函数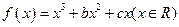 ,已
,已 知
知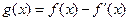
是奇函数.
(Ⅰ)求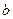 、
、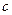 的值;
的值;
(Ⅱ)求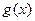 的单调区间与极值.
的单调区间与极值.