设
是奇函数，
是偶函数，并且
，求和表达式。
已知等式
，
其中ai（i=0，1，2，…，10）为实常数．
求：（1）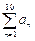
的值；（2）
的值．
是否存在自然数
，使得
对任意自然数
，都能被
整除，若存在，求出
的最大值，并证明你的结论；若不存在，说明理由．
已知矩阵
，向量
.
（1）求矩阵
的特征值
、
和特征向量
、
；
（2）求
的值.
（本小题满分16分：4+5+7）
已知函数
，其中e为常数，
（ｅ＝２．７１８２８．．．），
（1）当a=1时，求
的单调区间与极值；
（2）求证：在（1）的条件下，
（3）是否存在实数
，使最小值为3，若存在，求出的值，若不存在，说明理由。
（本小题满分16分：８＋８）
给出函数封闭的定义：若对于定义域D内的任一个自变量
，都有函数值
,则称函数y=f（x）在 D上封闭。
（1）若定义域
判断下列函数中哪些在
上封闭，并给出推理过程；
（2）若定义域
是否存在实数
，使函数
在
上封闭，若存在，求出值，若不存在，请说明理由。