(本题10分)如图,在四边形ABCD中,AB=2,CD=1,∠A=61°,
∠ADC=∠B=90°,利用解直角三角形知识求这个四边形ABCD的面积。
(结果精确到0.1。下列数据供参考: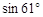 ≈0.87,
≈0.87,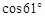 ≈0.48,
≈0.48,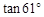 ≈1.80;
≈1.80;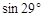 ≈0.48,
≈0.48,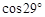 ≈0.87,
≈0.87,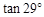 ≈0.55)
≈0.55)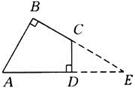
为了治理大气污染,我国中部某市抽取了该市2014年中120天的空气质量指数,绘制了如下不完整的统计图表:
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a=,m=;
(2)请把空气质量指数条形统计图补充完整:
(3)若绘制“空气质量指数扇形统计图”,级别为“优”所对应扇形的圆心角是度;
(4)估计该市2014年(365天)中空气质量指数大于100的天数约有天.
小明想从“天猫”某网店购买计算器,经査询,某品牌A号计算器的单价比B型号计算器的单价多10元,5台A型号的计算器与7台B型号的计算器的价钱相同,问A、B两种型号计算器的单价分别是多少?
(1)计算: ;
;
(2)解不等式组: .
.
如图,已知二次函数 的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为
的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为 .
.
(1)求二次函数 的解析式及点B的坐标;
的解析式及点B的坐标;
(2)由图象写出满足 的自变量x的取值范围;
的自变量x的取值范围;
(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形?若存在,求出P的坐标;若不存在,说明理由.
去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?