如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A、D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O).
(1)求此抛物线的解析式;
(2)过点P作CB所在直线的垂线,垂足为点R;
①求证:PF=PR
②是否存在点P,使得△PFR为等边三角形;若存在,求出点P的坐标,若不存在,请说明理由.
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为点S,试判断△RSF的形状.
(1)在下列横线上用含有a,b的代数式表示相应图形的面积.
① ② ③ ④
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示: ;
(3)利用(2)的结论计算9972+6×997+9的值.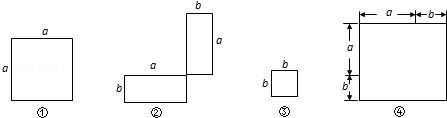
定义一种新运算:观察下列式:
1⊙3=1×4+3=7 3⊙(-1)=3×4-1=11 5⊙4=5×4+4=24 4⊙(-3)=4×4-3=13
(1)请你想一想:a⊙b= ;
(2)若a≠b,那么a⊙b b⊙a(填入“=”或“≠”)
(3)若a⊙(-2b)=4,请计算 (a-b)⊙(2a+b)的值.
在抗洪抢险中,人民解放军的冲锋舟沿东西方向的河流抢救灾民,早晨从A地出发,晚工到达B地,约定向东为正方向,当天航行路程记录如下:14,-9,-18,-7,13,-6,10,-5(单位:千米).
(1)B地在A地何位置?
(2)若冲锋舟每千米耗油0.5升,出发前冲锋舟油箱有油29升,求途中需补充多少升油?
把下列各数:-2.5,(-1)2,0,-|-2|,-(-3)在数轴上表示出来,并用“<”把它们连接起来.
小明买了张100元的乘车IC卡,如果他乘车的次数用x表示,则记录他每次乘车后的余额y元)如表:
| 次数x |
1 |
2 |
3 |
4 |
… |
| 余额y |
100-1.2 |
100-2.4 |
100-3.6 |
100-4.8 |
… |
(1)写出乘车的次数x表示余额y的关系式.
(2)利用上述关系式计算小明乘了15次车还剩下多少元?
(3)余额还有40元时,小明已使用此卡乘车多少次?
(4)小强最多能乘几次车?