已知 其中
其中 .(1)求函数
.(1)求函数 的单调区间;(2)若函数
的单调区间;(2)若函数 在区间
在区间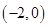 内恰有两个零点,求
内恰有两个零点,求 的取值范围;
的取值范围;
(3)当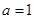 时,设函数
时,设函数 在区间
在区间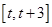 上的最大值为
上的最大值为 最小值为
最小值为 ,记
,记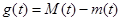 ,求函数
,求函数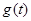 在区间
在区间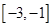 上的最小值.
上的最小值.
如图,ΔABC中,∠A=90°,AB=4,AC=3,平面ABC外一点P在平面ABC内的射影是AB中点M,二面角P—AC—B的大小为45°.
(I)求二面角P—BC—A的正切值;
(II)求二面角C—PB—A的正切值.
设 是等差数列,
是等差数列,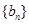 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且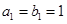 ,
,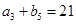 ,
,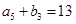 .
.
(Ⅰ)求 ,
,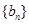 的通项公式;
的通项公式;
(Ⅱ)求数列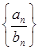 的前n项和
的前n项和 .
.
已知函数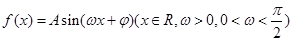 的部分图像如图所示.
的部分图像如图所示.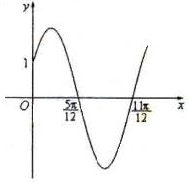
(Ⅰ)求函数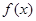 的解析式;
的解析式;
(Ⅱ)求函数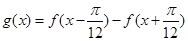 的单调递增区间.
的单调递增区间.
在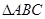 中,已知角
中,已知角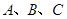 所对的边分别是
所对的边分别是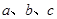 ,边
,边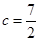 ,且
,且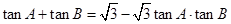 ,又
,又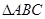 的面积为
的面积为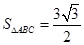 ,求
,求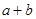 的值.
的值.
(本小题满分14分)
设函数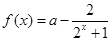 ,
,
(1)求证:不论 为何实数
为何实数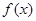 在定义域上总为增函数;
在定义域上总为增函数;
(2)确定 的值,使
的值,使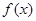 为奇函数;
为奇函数;
(3)当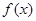 为奇函数时,求
为奇函数时,求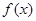 的值域.
的值域.