如图:在⊙O中,经过⊙O内一点P有一条弦AB,且AP=4,PB=3,过P点另有一动弦CD,连结AC,DB.设CP=x,PD=y.
(1)求证:△ACP∽△DBP;
(2)求y关于x的函数解析式;
(3)若CD=8时,求S△ACP:S△DBP的值.
在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF=. 
(本题12分)已知在长方形ABCD中,AB=4,BC=252,O为BC上一点,BO=72,如图所示,以BC所在直线为x轴,O为坐标原点建立平面直角坐标系,M为线段OC上的一点.
(1)若点M的坐标为(1,0),如图①,以OM为一边作等腰△OMP,使点P在长方形ABCD的一边上,则符合条件的等腰三角形有几个?请直接写出所有符合条件的点P的坐标;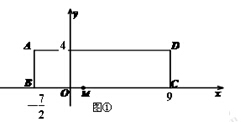
(2)若将(1)中的点M的坐标改为(4,0),其它条件不变,如图②,那么符合条件的等腰三角形有几个?求出所有符合条件的点P的坐标;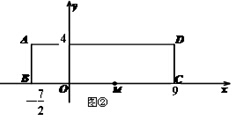
(3)若将(1)中的点M的坐标改为(5,0),其它条件不变,如图③,请直接写出符合条件的等腰三角形有几个.(不必求出点P的坐标)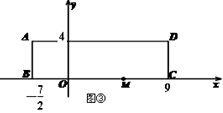
(本题12分)如图1,在长方形ABCD中,AB=12cm,BC=6cm,点P从A点出发,沿
A→B→C→D路线运动,到D点停止;点Q从D点出发,沿D→C→B→A运动,到A点停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒b(cm),点Q的速度变为每秒c(cm).如图2是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图3是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.根据图象: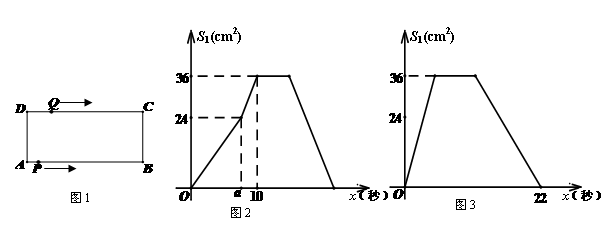
(1)请直接写出a=、b=、c=;
(2)设点P离开点A的运动路程为y1(cm),点Q到点A还需要走的路程为y2(cm),请分别写出改变速度后y1、y2与出发后的运动时间x(秒)的函数表达式,并求出P与Q相遇时x的值.
(本题12分)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
(本题10分)已知一次函数y=kx+b的图像经过点(-1,-2),且与正比例函数y= x的图像相交于点(2,a).
x的图像相交于点(2,a).
(1)求a、b、k的值;
(2)在图中画出这两个函数图像,并求这两个函数图像与x轴所围成的三角形面积.