如图所示,一根长为L=1.5m的绝缘细直杆MN,竖直固定在场强为E=1.0×105N/C、与水平方向成θ=37°角的倾斜向上的匀强电场中.杆的下端M固定一个带电小球A,电荷量Q= +4.5×10-6C;另一带电小来自球B穿在杆上可自由滑动,电荷量q= +1.0×10-6C,质量m=1.0×10-2kg,与杆之间的动摩擦因数μ=0.1.现将小球B从杆的上端N静止释放,小球B开始运动.(静电力常量k=9.0×109N·m2/C2.取g=10m/s2,sin37°=0.6,cos37°=0.8)

(1)小球B开始运动时的加速度为多大?
(2)小球B的速度最大时,距M端的高度h为多大?
(3)若小球B在下落过程的最大速度为0.77m/s,则从开始下落到速度达到最大的过程中,小球B的电势能改变了多少?
“抗震救灾,众志成城”,2008年5月15日成都军区向汶川等灾区空投包括5万份干粮、2.5万双军用胶鞋、0.5万床棉被在内的救灾物资.直升飞机沿水平方向匀速飞往救灾物资集结地.图示为悬挂着m=500kg空箱的悬索与竖直方向的夹角θ1=45º;而直升机载上救灾物资飞往灾区时,加速度沿水平方向,大小稳定在a=1.5m/s2,悬索与竖直方向的夹角θ2=14º.若空气阻力大小不变,且忽略悬索的质量.(重力加速度g=10m/s2,tan14 º=0.25)
试求: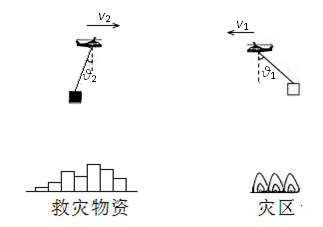
空气阻力的大小;
箱中救灾物资的质量.
如图所示,一光滑的曲面与长L=2m的水平传送带左端平滑连接,一滑块从曲面上某位置由静止开始下滑,滑块与传送带间的动摩擦因数μ="0" .5,传送带离地面高度h0=0.8m。重力加速度g=10m/s2。
若传送带固定不动,滑块从曲面上离传送带高度h1="1." 8m的A处开始下滑,求滑块落地点与传送带右端的水平距离;
若传送带以速率v0=5m/s顺时针匀速转动,求滑块在传送带上运动的时间。
如图所示,1、2两细绳与水平车顶的夹角分 别为300和600,物体质量为m,现让小车以2g(g为重力加速度)的加速度向右做匀加速直线运动,当物体与车保持相对静止时,求:绳1中弹力的大小?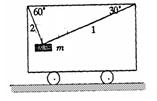
下面是一位同学的解法
解:以物体m为研究对象,受力分析如图,由牛顿第二定律得:
x:T1cos300-T2cos600=ma
y:T1sin300 +T2sin600=mg
解得: T1=(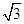 +
+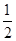 )mg
)mg
你认为该同学的解法正确吗?如有错误请写出正确的解法。
如图所示,匀强电场区域和匀强磁场区域是紧邻的且宽度相等均为d,电场方向在纸平面内,而磁场方向垂直纸面向里.一带正电粒子从O点以速度v0沿垂直电场方向进入电场.在电场力的作用下发生偏转,从A点离开电场进入磁场,离开电场时带电粒子在电场方向的偏移量为d,当粒子从C点穿出磁场时速度方向与进入电场O点时的速度方向一致,不计带电粒子的重力,求:
粒子从C点穿出磁场时的速度v.
电场强度和磁感应强度的比值.
如图所示的电路中,电源电动势E =" 6.0V" ,内阻r =" 0.6Ω" ,电阻R2 =" 0.5Ω" ,当开关S断开时,电流表的示数为1.5A,电压表的示数为3.0V ,试求:
电阻R1和R3的阻值
当S闭合后,求电压表的示数和R2上消耗的电功率