某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件.经调查发现,这种商品的销售单价每提高1元,其销售量相应减少10件.将销售价定为多少时,才能使每天所获销售利润最大?最大利润是多少?
如图,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm.点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.
(1)试写出△PBQ的面积S(cm2)与动点运动时间t(s)之间的函数表达式;
(2)运动时间t为何值时,△PBQ的面积最大?最大值是多少?
已知函数 (
( 为常数).
为常数).
(1)证明:无论m取何值,该函数与 轴总有两个交点;
轴总有两个交点;
(2)设函数的两交点的横坐标分别为 和
和 ,且
,且 ,求此函数的解析式.
,求此函数的解析式.
某旅行社为了吸引游客组团去旅游,推出了如下收费标准:
(1)若A单位组织该单位25名员工去旅游,需支付给该旅行社旅游费用_____元。
(2)若B单位共支付给该旅行社旅游费用27000元,请问B单位共有多少名员工去旅游?
知识迁移
当 且
且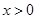 时,因为
时,因为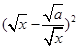 ≥
≥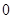 ,所以
,所以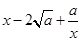 ≥
≥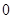 ,从而
,从而 ≥
≥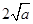 (当
(当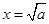 时取等号).记函数
时取等号).记函数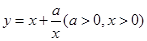 ,由上述结论可知:当
,由上述结论可知:当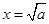 时,该函数有最小值为
时,该函数有最小值为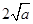 .
.
直接应用
已知函数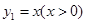 与函数
与函数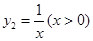 ,则当
,则当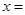 时,
时,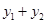 取得最小值为 .
取得最小值为 .
变形应用
已知函数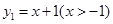 与函数
与函数 ,求
,求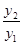 的最小值,并指出取得该最小值时相应的
的最小值,并指出取得该最小值时相应的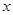 的值.
的值.
实际应用
已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共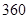 元;二是燃油费,每千米为
元;二是燃油费,每千米为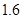 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为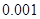 .设该汽车一次运输的路程为
.设该汽车一次运输的路程为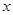 千米,求当
千米,求当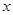 为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
已知关于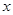 的一元二次方程
的一元二次方程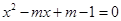 的两个实数根
的两个实数根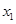 、
、 的值分别是□ABCD的两边AB、AD的长.
的值分别是□ABCD的两边AB、AD的长.
(1)如果 ,试求□ABCD的周长;
,试求□ABCD的周长;
(2)当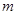 为何值时,□ABCD是菱形?
为何值时,□ABCD是菱形?