知识迁移
当 且
且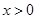 时,因为
时,因为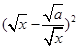 ≥
≥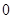 ,所以
,所以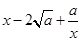 ≥
≥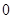 ,从而
,从而 ≥
≥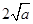 (当
(当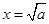 时取等号).记函数
时取等号).记函数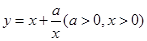 ,由上述结论可知:当
,由上述结论可知:当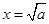 时,该函数有最小值为
时,该函数有最小值为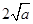 .
.
直接应用
已知函数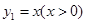 与函数
与函数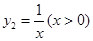 ,则当
,则当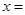 时,
时,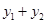 取得最小值为 .
取得最小值为 .
变形应用
已知函数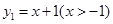 与函数
与函数 ,求
,求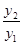 的最小值,并指出取得该最小值时相应的
的最小值,并指出取得该最小值时相应的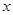 的值.
的值.
实际应用
已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共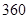 元;二是燃油费,每千米为
元;二是燃油费,每千米为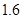 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为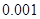 .设该汽车一次运输的路程为
.设该汽车一次运输的路程为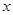 千米,求当
千米,求当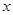 为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
如图,已知A(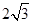 ,2)、B(
,2)、B(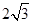 ,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2,
,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2,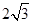 )的位置,B旋转到点B′位置
)的位置,B旋转到点B′位置
(1)求B′点坐标.
(2)求阴影部分面积。
在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x+1的图象上的概率;
(3)在平面直角坐标系xOy中,⊙O的半径是2,求过点M(x,y)能作⊙O的切线的概率.
如图,A、B是双曲线y= 上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,过B点作BE⊥x轴,垂足为E.若△ADO的面积为1,D为OB的中点,
上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,过B点作BE⊥x轴,垂足为E.若△ADO的面积为1,D为OB的中点,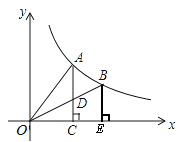
(1)求四边形DCEB的面积。
(2)求k的值。
(1)解方程:x2﹣2x﹣2=0
(2)解方程:.4(x+3)2=25(x﹣2)2.
如图1,直线l交x轴、y轴分别于A、B两点,A(a,0),B(0,b),且(a-b)2+|b-4|=0.
(1)求A、B两点坐标;
(2)如图2,C为线段AB上一点,且C点的横坐标是3.求△AOC的面积;
(3)如图2,在(2)的条件下,以OC为直角边作等腰直角△POC,请求出P点坐标;
(4)如图3,在(2)的条件下,过B点作BD⊥OC,交OC、OA分别于F、D两点,E为OA上一点,且∠CEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.