(本小题满分12分)a2,a5是方程x 2-12x+27=0的两根,数列{ }是公差为正数的等差数列,数列{
}是公差为正数的等差数列,数列{ }的前n项和为
}的前n项和为 ,且
,且 =1-
=1-
(1)求数列{ },{
},{ }的通项公式;
}的通项公式;
(2)记 =
=
 ,求数列{
,求数列{ }的前n项和Sn.
}的前n项和Sn.
(本小题满分10分)
已知椭圆的中心在原点,焦点在 轴上,离心率为
轴上,离心率为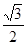 ,且经过点
,且经过点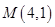 ,直线
,直线 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B.
(1)求椭圆的方程;
(2)求 的取值范围。
的取值范围。
(本小题满分12分)设函数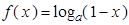 ,
, (
( 且
且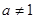 )。
)。
(1)设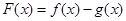 ,判断
,判断 的奇偶性并证明;
的奇偶性并证明;
(2)若关于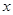 的方程
的方程 有两个不等实根,求实数
有两个不等实根,求实数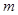 的范围;
的范围;
(3)若 且在
且在 时,
时,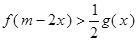 恒成立,求实数
恒成立,求实数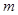 的范围。
的范围。
(本题满分12分) 设 是定义在
是定义在 上的增函数,令
上的增函数,令
(1)求证 时定值;
时定值;
(2)判断 在
在 上的单调性,并证明;
上的单调性,并证明;
(3)若 ,求证
,求证 。
。
(本小题12分)已知函数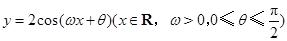 的图象与
的图象与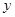 轴相交于点M
轴相交于点M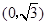 ,
,
且该函数的最小正周期为 .
.
(1)求 和
和 的值;
的值;
(2)已知点 ,点
,点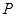 是该函数图象上一点,点
是该函数图象上一点,点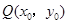 是
是 的中点,当
的中点,当 ,
,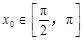 时,求
时,求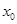 的值。
的值。
(本小题满分12分)已知 为圆
为圆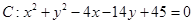 上任一点,且点
上任一点,且点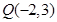 .
.
(1)若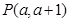 在圆
在圆 上,求线段
上,求线段 的长及直线
的长及直线 的斜率;
的斜率;
(2)求 的最大值和最小值;
的最大值和最小值;
(3)若 ,求
,求 的最大值和最小值.
的最大值和最小值.