某校为了探索一种新的教学模式,进行了一项课题实验,乙班为实验班,甲班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,成绩如下表(总分:150分):
甲班
| 成绩 |
 |
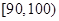 |
 |
 |
 |
| 频数 |
4 |
20 |
15 |
10 |
1 |
乙班
| 成绩 |
 |
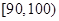 |
 |
 |
 |
| 频数 |
1 |
11 |
23 |
13 |
2 |
(1)现从甲班成绩位于 内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
(2)根据所给数据可估计在这次测试中,甲班的平均分是101.8,请你估计乙班的平均分,并计算两班平均分相差几分;
(3)完成下面2×2列联表,你认为在犯错误的概率不超过0.025的前提下, “这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由。
| |
成绩小于100分 |
成绩不小于100分 |
合计 |
| 甲班 |
 |
26 |
50 |
| 乙班 |
12 |
 |
50 |
| 合计 |
36 |
64 |
100 |
附:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分12分)已知等差数列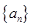 的公差
的公差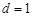 ,前
,前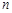 项和为
项和为 .
.
(1)若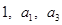 成等比数列,求
成等比数列,求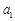 ;
;
(2)若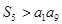 ,求
,求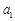 的取值范围.
的取值范围.
(本小题满分10分)若不等式 的解集是
的解集是 ,求不等式
,求不等式 的解集.
的解集.
(本小题满分12分)已知:函数 对一切实数
对一切实数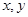 都有
都有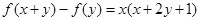 成立,且
成立,且 .
.
(1)求 的值;
的值;
(2)求 的解析式;
的解析式;
(3)已知 ,设
,设 :当
:当 时,不等式
时,不等式 恒成立;
恒成立; :当
:当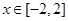 时,
时,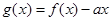 是单调函数.如果满足
是单调函数.如果满足 成立的
成立的 的集合记为
的集合记为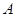 ,满足
,满足 成立的
成立的 的集合记为
的集合记为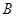 ,求
,求 (
( 为全集).
为全集).
(本小题满分12分)某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)求在这10个卖场中,甲型号电视机的“星级卖场”的个数;
(2)若在这10个卖场中,乙型号电视机销售量的平均数为26.7,求 的概率;
的概率;
(3)若a=1,记乙型号电视机销售量的方差为 ,根据茎叶图推断b为何值时,
,根据茎叶图推断b为何值时, 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
(本小题满分12分)数列{ }的前
}的前 项和为
项和为 ,
, 是
是 和
和 的等差中项,等差数列{
的等差中项,等差数列{ }满足
}满足 ,
, .
.
(1)求数列 ,
,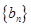 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列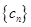 的前
的前 项和
项和 .
.